第１５問の解答

---

１．問題

ｎ個の碁石が並んでいます。 次のルールで、２人が碁石を交互に取っていきます。 個数はあらかじめ分かっています。 交互に１個か、または連続した２個の碁石を取っていきます。 （ルールＡ）最後に石を取ったほうが勝ちとします。 （ルールB）最後に石を取ったほうが負けとします。 このゲームでは、先手、後手とも最善の手をとっていくと、最初のｎの値によって 　　・先手が必ず勝つ手順がある（先手必勝） 　　・後手が必ず勝つ手順がある（後手必勝） の２通りに分かれます。 （１）ルールＡでゲームをした場合、１≦ｎ≦９のとき、 　　後手必勝となるのはｎがいくつといくつのときでしょうか？ （２）ルールＢでゲームをした場合、１≦ｎ≦９のとき、 　　後手必勝となるのはｎがいくつといくつのときでしょうか？ （参考）JavaScriptを用いてゲームができます。

---

２．解答例１(清川育男さん、ちゃめさん、サンデー毎日願望男さん、tomhさん、ありさのお父さん他)

（設問１）

結論からいうと、全ての場合で先手必勝になります。

先手の取る必勝手は次の通り。

• 先手：
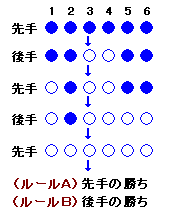
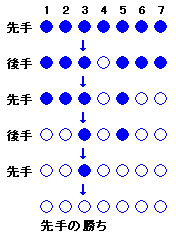
  　先手は最初の碁石数が奇数なら１個、偶数なら２個だけ真ん中の碁石を取ります。
• 後手：
  　左右に分かれたどちらか一方から１個または２個とります。
• 先手：
  　後手が取った碁石と対称の位置にある碁石をとります。
• 以下同様にして、最後の石は必ず先手が取ることとなりますので、先手必勝です。

（設問２）

結論からいうと、１、４、９個が後手必勝になります。

第１４問の補足と同様にして帰納法で考えます。

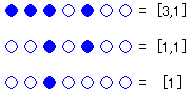
残った碁石の状態を、連続した石の個数を大きい順に並べて、

のように表すこととします。

下表で、青色は先手必勝、赤色は後手必勝を表します。

各状態の上にマウスを置くと次の手を、
　先手必勝の場合は、後手必勝となるものを１手だけ、
　後手必勝の場合は、次の手（全て先手必勝）を全て
とその手の判定結果を下の欄に表示します。

0	[0]	-
1	[1]	-
2	[2]	[1,1]
3	[3]	[2,1] [1,1,1]
4	[4]	[3,1] [2,2] [2,1,1] [1,1,1,1]
5	[5]	[4,1] [3,2] [3,1,1] [2,2,1] [2,1,1,1] 以下略
6	[6]	[5,1] [4,2] [4,1,1] [3,3] [3,2,1] 以下略
7	[7]	[6,1] [5,2] [4,3] 以下略
8	[8]	[7,1] [6,2] [5,3] [4,4] 以下略
9	[9]	省略

---