第20問の解答
1.問題
| 4個の正の整数があります。 これらの整数から2個ずつ取り出して積を計算すると6個の異なる整数を得ました。 これらを小さい順にならべると、6,10,14,15,21,35になりました。 では、4個の正の整数はいったいどんな整数だったのでしょうか? (おまけ) |
2.解答例1(tomhさん、清川育男さん、ちゃめさん、津田俊明さん、ありさのお父さん他)
6個の数字を二つの整数の積で表します。
6= 1× 6
= 2× 310= 1×10
= 2× 514= 1×14
= 2× 715= 1×15
= 3× 521= 1×21
= 3× 735= 1×35
= 5× 7このうち、因数に1があると、相棒の数字が他にも現われなければならない(例えば、6=1×6とすると、6が他に二つ現われてなければならない)が、そのような数字は一つもない。
よって、1を含まない方が、正しい答である:2、3、5、7。
実際、これら四つの数字は六つの積の中に3回ずつ現われているので題意を満たす。
以上
(おまけ)
6つの積を素因数分解すると、
23×3、25、24×3、23×32、22×33、24×32
となります。全部かけると、221×39=(27×33)3となるので、4数の積は27×33となります。
つまり、4つの数に2を7つ、3を3つ割り当てれば良いことになります。3のべきが1個の数が2つ(23×3、24×3)あるので、1つの数には3を1つだけ割り当てることになります。
3が1つ割り当てられる数が更に存在すれば、3のべきが1個の数は1つしかできないので、1つの数に3を2つ(つまり9)を割り当てます。
3のべきが3個になっている数(22×33)は、これら2つの数の積なので、この2数併せて2が2つ割り当てられます。
そして、3が1つ(23×3、24×3)と3が2つ(23×32、24×32)の数の他の素因数(23、24)を見ると同じなので、この2数には2が1つずつ割り当てられます。
これで4つの元数のうち2数は、6と18と決まりました。
残る2数の積は25ですが、24をつくる必要から1つは4、残りが8と決まります。したがって小さい方から順に並べると 4,6,8,18 となります。
(別解)
6個の数字を整数の積で表します。
24= 1× 24
= 2× 12
= 3× 8
= 4× 6
32= 1×32
= 2×16
= 4× 8
48= 1×48
= 2×24
= 3×16
= 4×12
= 6× 872= 1×72
= 2×36
= 3×24
= 4×18
= 6×12
= 8× 9108= 1×108
= 2× 54
= 3× 36
= 4× 27
= 6× 18
= 9× 12144= 1×144
= 2× 72
= 3× 48
= 4× 36
= 6× 24
= 8× 18
=12× 1232=1×32とすると、1,32が元の2数となるが、32を因数に持つものは他にないので不適。
32=2×16とすると、2,16が元の2数となるが、16を因数に持つものは他に3×16、8×16となるので、残りの2数が3、8となるが題意を満たさない。
32=4×8とすると、4,8が元の2数となる。
24=1×24、2×12、3×8のいずれかとすると、1,2,3が元の数になるが、4との積、1×4、2×4、3×4とも6つの積の中にないので不適。
よって、24=4×6となり、6が元の数になる。最後の数は、72,108,144のそれぞれの共通因数である18となる。
3.解答例2(Hamayanさん、ちゃめさん、K.Kさん他)
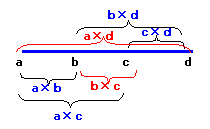
4つの整数を小さい順にa,b,c,dとします。
a×b<a×c<b×c<b×d<c×d、およびa×b<a×c<a×d<b×d<c×d
より、a×b=6、a×c=10、b×d=21、c×d=35・・・(1)となります。
よって、(a×c)/(a×b)=c/b=5/3 ・・・(2)となります。
b×c<a×dと仮定すると、b×c=14、a×d=15・・・(3) となるが、
(2)×(3)より、c2=70/3となり不適。a×d<b×cと仮定すると、a×d=14、b×c=15 ・・・(4)となり、
(2)×(4)より、c2=25となりc=5。(2)より、b=3となり、(1)より、a=2、d=7となる。
答a=2、b=3、c=5、d=7
以上
(おまけ)
同様の議論で、
a×b=24、a×c=32、b×d=108、c×d=144・・・(1)’となります。よって、(a×c)/(a×b)=c/b=4/3 ・・・(2)’となります。
b×c<a×dと仮定すると、b×c=48、a×d=72・・・(3)’ となるが、
(2)’×(3)’より、c2=64となりc=8。(2)’より、b=6となり、(1)’より、a=4、d=18となる。
a×d<b×cと仮定すると、a×d=48、b×c=72 ・・・(4)’となり、
(2)’×(4)’より、c2=96となり不適。
答a=4、b=6、c=8、d=18