第２１問の解答

１．問題


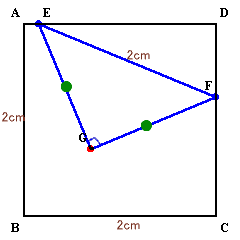１辺が２ｃｍの正方形ＡＢＣＤと斜辺の長さが２ｃｍの直角２等辺三角形ＥＦＧがあります。

三角形ＥＦＧを頂点Ｅ、Ｆが正方形ＡＢＣＤの周上にあるようにして１周動かしたとき、頂点Ｇが動く軌跡の長さ(頂点がたどる道のりの長さ)を求めて下さい。

　

２．解答例1


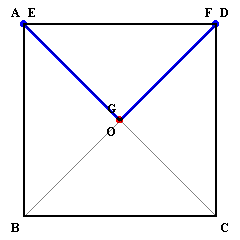
実際に動かしてみると図１のように、Ｇは十字形を描くようです。

図１
参考図1

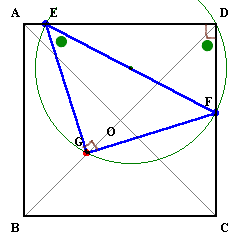
ＧがＡＤ上、ＥがＣＤ上にあるとします。

参考図2

∠ＥＤＦ＝∠ＥＧＦ＝∠Ｒ（直角）だから、四角形ＥＧＦＤは円に内接します。

すると、円周角より∠ＧＤＦ＝∠ＤＥＦ＝４５°となり、Ｇは対角線ＢＤ上にあることが分かります。

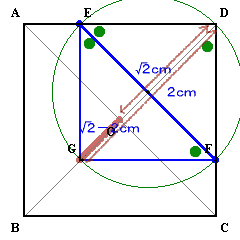
ＧＤが最大になるのは、ちょうどＧＤが円の直径になるとき、すなわちＥがＡＤの中点、∠ＧＥＤ＝∠Ｒとなるときである。このとき、ＧＤ＝ＥＦ＝２ｃｍとなります。

参考図3

また、ＤはＯＢ上にありますので、ＧＤが最小になるのは、Ｇが対角線の交点Ｏと重なるとき、すなわちＥがＡまたはＤと重なるときである。このとき、ＧＤ＝ＥＧ＝√２ｃｍとなります。

この間、Ｇは（２−√２）の長さの線分を往復しますので、△ＥＦＧが正方形上を１周すると、たどる道のりは、（２−√２）×２×４＝１６−８√２ｃｍとなります。

以上