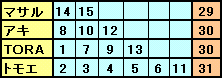
第23問の解答
1.問題
マサル君、TORA君、トモエさん、アキ君の小学生4人が15枚のカードを分け合いました。カードには1、2、・・・、15までの異なる整数を書いてあります。
では、トモエさんの持っているカード枚数とカードに書かれている数字を求めて下さい。 |
2.解答例1(サンデー毎日願望男さん、Taroさん、ちゃめさん他)
(1)
1+2+3+・・・・・+15=120、 120/4=30より合計数の一番多いトモエさんの合計数は31以上ですから、それより2少ないマサル君の合計数は29以上となります。(2)
もし、マサル君の合計数が30以上なら、全員の合計は30×4+2=122以上となりますので、不適。よって、マサル君の合計=29、トモエさんの合計=31、残りの二人の合計はそれぞれ30と分かります。
(3)
カードの数は15までなので、一番少ない枚数がマサル君で合計数が29となるためには、マサル君はカードは最低2枚は持っていることになります。
(4)
4人が持っているカードの枚数は皆違っており、合計数が15枚、最低数が2枚であることから、4人が持っているカードの枚数は、少ない方から2枚(マサル君)、3枚、4枚、6枚(トモエさん)となります。(5)
上の(1)、(2)、(3)からマサル君は14、15の2枚となります。(6)
TORA君は3枚か4枚持っていますが、奇数ばかりですので3枚では合計数が30になりません。従って、4枚です。よって、アキ君が3枚持っていることとなります。
(7)
アキ君の3枚は偶数ばかりで、14はマサル君が持っていますので、全て12以下。ところが、12+10+8=30なので、8、10、12の3枚と分かります。(8)
TORA君は7以外に奇数ばかり3枚持って合計30なので、残り3枚の合計は23。(9)
15はマサル君が持っていることから、1、3、5、9、11、13のうち3枚で合計数が23となるのを考えると、1、9、13、および3、9、11の2通りがありますが、3、9、11のときは、トモエさんが13を持つことになり、小学生のトモエさんの「私の年齢より大きい数はない」からありえません。よって、TORA君は1、7、9、13の4枚と決まります。
(10)
以上から、マサル君は残りのカードの2、3、4、5、6、11の6枚となります。
答:(1)6枚 (2)2、3、4、5、6、11
以上