第２４問の解答

---

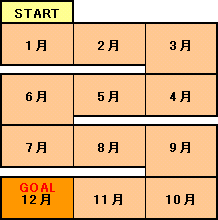
１．問題

左図のようなすごろくがあり、さいころをころがして、出た目の数だけ駒を進めます。後戻りはありません。 従って、例えば８月にいるとき、出た目が４以上ならゴールになります。 では、駒の進め方は全部で何通りあるでしょう。

---

２．解答例1

（Taroさん、カミナリ親父さん、Hamayanさん、文堂のＪａｃｋ先生さん、清川育男さん、tomhさん、ノースダウンさん他）

ちょうどｎマス目に到達する場合の数をｆ（ｎ）とします。
直前にあったマス目が、

• （ｎ−６）にあったとき、サイコロの目が６
• （ｎ−５）にあったとき、サイコロの目が５
• （ｎ−４）にあったとき、サイコロの目が４
• （ｎ−３）にあったとき、サイコロの目が３
• （ｎ−２）にあったとき、サイコロの目が２
• （ｎ−１）にあったとき、サイコロの目が１

であればいいので、
　ｆ（ｎ）＝ｆ（ｎ−６）＋ｆ（ｎ−５）＋ｆ（ｎ−４）＋ｆ（ｎ−３）＋ｆ（ｎ−２）＋ｆ（ｎ−１）
が成り立ちます。
ただし、ｎ＜０のとき、ｆ（ｎ）＝０、ｆ（０）＝１と考えます。

この漸化式によって、計算すると下表のようになります。

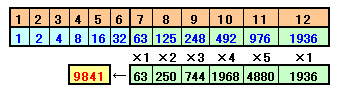
• ちょうどゴールに達する場合：上表のように１９６３通り

• 直前が７月で、サイコロの目が６の場合：６３×１＝６３通り

• 直前が８月で、サイコロの目が５〜６の場合：１２５×２＝２５０通り

• 直前が９月で、サイコロの目が４〜６の場合：２４８×３＝７４４通り

• 直前が１０月で、サイコロの目が３〜６の場合：４９２×４＝１９６８通り

• 直前が１１月で、サイコロの目が２〜６の場合：９７６×５＝４８８０通り
  
  合計、１９６３＋６３＋２５０＋７４４＋１９６８＋４８８０＝９８４１通りになります。

答：９８４１通り

以上

---