第25問の解答
1.問題
| kuriさんは、3人の子供におみやげを買おうと思っておもちゃ店にいきました。 良さそうなおもちゃが5個見つかったので、このうちの3個を選んでちょうど5000円にしようと思いました。 しかしながら、一生懸命計算してみると、3個の合計金額は、 では、5個のおもちゃの値段を答えて下さい。 |
2.解答例1
(カミナリ親父さん、ありっちさん、勢見賢人さん、Taroさん、SPACYさん、山さん他)
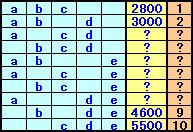
5個の中から3個選ぶのは、下表のように10通りあります。
ここで、おもちゃの価格で同じものがもしあれば、3個の合計金額は最大7通りにしかならないことが分かるので、全て価格は異なることになります。
このうち、a+b+cが最も価格が安く、a+b+dがその次に安いことが分かります。
また、一番高いのがc+d+eで、その次がb+d+eになります。従って、
a+b+c=2800 ・・・ (1)
a+b+d=3000 ・・・ (2)
b+d+e=4600 ・・・ (3)
c+d+e=5500 ・・・ (4)
が成り立ちます。(2)−(1)より、d−c=2000
(4)−(3)より、c−b=900
よって、b=c−900、d=c+2000。
これらを、(1)、(4)に代入して、a=3700−2c、e=4600−2cを得ます。
a=3700−2c ・・・ (5)
b=c−900 ・・・ (6)
c=c
d=c+200 ・・・ (7)
e=4600−2c ・・・ (8)(6)、(7)より、 b+c+d=3c−700 ・・・ 3で割った余り2 ・・・ (9)
9通りある合計金額のうち、組合わせの分かった(1)から(4)を除く5通りについて、3で割った余りを求めると、
3300 ・・・ 余り0 ・・・ (10)
3900 ・・・ 余り0 ・・・ (11)
4100 ・・・ 余り2 ・・・ (12)
4200 ・・・ 余り0 ・・・ (13)
4400 ・・・ 余り2 ・・・ (14)
となる。(余りは、各桁の数字の合計からすぐに求まる)従って、b+c+d=3c−700は、4100または4400のいずれか。
3c−700=4100 のとき c=1600 ・・・ (15)
3c−700=4400 のとき c=1700 ・・・ (16)(5)〜(8)より、
i. c=1600のとき、a=500、b=700、c=1600、d=1800、e=2100
ii. c=1700のとき、a=300、b=800、c=1700、d=1900、e=1900iは、d=e=1900になって不適。
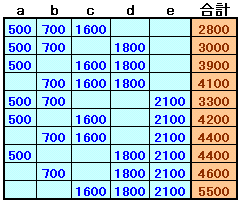
iiは、3個すづの合計金額を計算すると、下表のようになって題意に適する。
答:500円、700円、1600円、1800円、2100円
以上
3.解答例2(ノースダウンさん、清川育男さん、吉田和義さん他)
(1)〜(8)を得るまでは、解答例1と同様。
ここで、5個の中から3個選ぶのは10通りあるのに、合計金額が9通りしかないことから、等しいものが1組あることが分かります。それを、s0円とします。
10通りの合計金額(s0の重複を含む)を計算すると、
6a+6b+6c+6d+6e=35800+s0
s0=6s−35800=6(s−596)+2 ・・・ (17)
となり、s0は6で割った余りが2となります。ところが実際に9通りある合計金額を、それぞれ6で割った余りは、
2800 ・・・ 余り4
3000 ・・・ 余り0
3300 ・・・ 余り0
3900 ・・・ 余り0
4100 ・・・ 余り2
4200 ・・・ 余り0
4400 ・・・ 余り2
4600 ・・・ 余り4
5500 ・・・ 余り4
なので、s0=4100、4400のいづれかになります。(17)より、s=(35800+s0)/6、
(1)+(4)より、(a+b+c+d+e)+c=8300、
よって、c=8300−s。
s0=4100のとき、s=6650、c=1650
s0=4400のとき、s=6700、c=1600もし、c=1650とすると、(9)より b+c+d=3c−700=4250 となり、
9通りある合計金額のいづれにも該当しないので不適。
よって、c=1600。以下、解答例1と同様にして、
a=500、b=700、c=1600、d=1800、e=2100
となる。以上