第２６問の解答

１．問題

ｋｕｒｉちゃんは、貯金箱に貯まったおこずかいを持ってお菓子屋さんに行きました。
合計２１１円のお菓子を買うことにしました。

１円玉、５円玉、１０円玉、５０円玉、１００円玉は沢山持っています。
おつりのないようにお金を払うのに、合計何通りあるでしょう？

（注）どんなに硬貨の枚数が多くても、お菓子屋さんは受け取ってくれます。
　　　１円玉を２１１枚でもＯＫです。

２．解答例1（Taroさん、清川育男さん、カミナリ親父さん、山さん、吉田和義さん、ありっちさん、tomhさん、northdownさん他）

２１１円のうち、２１０円を支払えば残りは１円玉１個と決まるので、２１０円で考えることにします。

（１）最初に１円玉、５円玉、１０円玉でＮ円（Ｎは１０の倍数）を支払う場合を考えます。

１０円玉、５円玉で支払った残りは、全て１円玉で支払うことになるので、Ｎ円のうち、１０円玉、５円玉を支払える場合を考えればいいことになります。

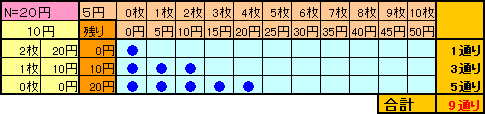
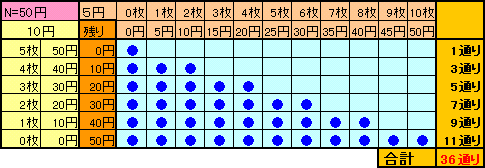
１０円玉は、Ｎ/10枚Ｎ円、１枚１０円、・・・、０枚０円の（Ｎ＋１）通りの支払い方があり、残りの金額は、０円、(Ｎ−１０)円、・・・、Ｎ円となります。

残り金額を５円玉で支払うのは、

  • ０円：０枚　・・　１通り

  • １０円：０、１、２枚　・・　３通り

  • ２０円：０、１、２、３、４枚　・・・　５通り
    　・・・・

  • Ｎ円：０、１、２、・・・、(2N-1)、２Ｎ枚　・・・　（２Ｎ＋１）通り

となるので、合計１＋３＋５＋・・・＋（２Ｎ＋１）＝（Ｎ/１０＋１）2通りとなります。

（Ｎ＝２０円、５０円の例）
参考図1
参考図2

（２）次に５０円玉、１００円玉で２１０円を支払う場合を考えます。

これは（１）の場合で、５円玉、１０円玉で２０円を支払う場合と同様、次の９通りあります。

参考図3

残り金額としては、１０円３通り、６０円２通り、１１０円２通り、１６０円１通り、２１０円１通りになるので、それぞれを１円玉、５円玉、１０円玉で支払う場合の数を（１）より求めると下記の通りとなる。

参考図4

従って、合計１２＋９８＋２８８＋２８９＋４８４＝１１７１通りとなります。

答：１１７１通り

以上