第27問の解答
1.問題
| セブンイレブン国では、7円玉と11円玉の硬貨のみ発行していて、紙幣は全く発行していません。
(問1)10000円以内の買い物で、お釣りのないように支払うことの出来る金額は何通りでしょうか。 (問2)10000円以内の買い物で、お釣りをもらうことも可能な場合に支払うことの出来る金額は何通りでしょうか。 |
2.解答例1(Taroさん、清川育男さん、吉田和義さん、カミナリ親父さん、N.Nishi さん、ありっちさん、他)
(問1)
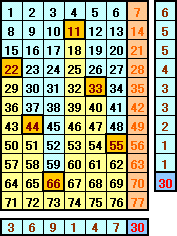
1円から7円まで、8円から14円まで、・・・、を表1のように並べます。
表1
表2
7の倍数、および11の倍数となる金額は、それぞれ1種類の硬貨だけで支払うことが出来ます。
次に、ある金額が7円玉、11円玉で支払うことが出来ると、その金額に7の倍数を加えた金額(すなわち表2の同じ列で下にあるもの)は全て支払うことが出来ます。
残った金額は、7円玉、11円玉だけでは支払うことができないので、これらの個数を数えると30通りになります。
よって、1円から10000円までで支払い可能な金額は10000−30=9970通りとなります。
(問2)
11×2−7×3=1なので、1円を支払うのには、11円玉を2枚だして7円玉を3枚をお釣りとして貰えばいいことになります。
よって、n円(n>1)のときも同様にして、11円玉をn枚だして7円玉をn枚をお釣りとして貰うといいことになります。
従って、1円以上の任意の金額を支払うことができるので、1万円までだと10000通りとなります。
答:(問1)9970通り (問2)10000通り
以上
3.解答例2(tomhさん、他)
まず、p円を7円玉m枚、11円玉n枚で払った(負のときはお釣りとして貰う)とすると、
7m +11n=p ・・・ (1)
となります。(1)の整数解のうち、m、nともに正の解の個数が問1、負の解もあって良いときが問2の個数となります。
p=1のとき、(1) を解いてみましょう。
7×(−3) +11×2=1 ・・・ (2)
より、m=−3、n=2が一つの解になります。
よって、m=−3p、n=2pは、(1)の一つの解になります。従って、お釣りが可能なら、全ての金額を支払うことが出来ますので、問2の答は10000通りになります。
更に(1)の一般解を求めましょう。
(1)−(2)×pより、
7(m+3p)+11(n−2p)=0
7(m+3p)=−11(n−2p) ・・・ (3)
7と11は互いに素なので、(3)より、(m+3p)は11の倍数、(n−2p)は7の倍数となります。よって、kを任意の整数としてm+3p=11k、n−2p=7k、
すなわち、m=11k−3p、n=−7k+2p ・・・ (4) と表せます。
問1の答を得るため、(1)が正の整数解を持つ条件を求めます。
(4)から、
m=11k−3p≧ 0,
n=−7k+2p ≧ 0
となり、
2/7×p ≧ k ≧ 3/11×p ・・・ (5)
を得ます。
(5)より、もし 2/7×p−3/11×p=1/77×p ≧ 1
すなわち、p ≧ 77ならば、必ず(5)は正の整数解を持ちますので、p<77を調
べれば十分なことがわかります。
以上、46通りです。これに77円〜10000円の9924通りを合わせる
と、計9970通りとなります。
(参考)
一般に、p、qが互いに素である正整数のとき、次が成り立つ。
(1)px+qy=1は、必ず整数解x、yを持つ。
(2)d≧pqのとき、px+qy=dは必ず正または0の整数解x、yを持つ。(証明)p>qとして一般性を失わない。
(1)
p、p×2、p×3、・・・、p×(q−1)、p×qについて、それぞれqで割った余りをr1、r2、r3、・・・、rq-1、rq・・・(A)とする。もし、(A)の中に等しいもの(rm=rn、1≦m<n≦q)があったと仮定する。
pm=qs+rm、pn=qt+rnと表せるので、
pm−pn=rm−rn=0、よってp(m−n)=0。
これは、m<nに反するので矛盾。
よって、(A)の中に等しいものはない。qで割った余りは、0、1、2、・・・、q−1のq個しかなく、(A)の個数は、q個なので、この中に1に等しいものが必ず存在する。これをrnとする。
pn=qt+rn=qt+1
pn+q(−t)=1 ・・・(B)
よって、px+qy=1は、整数解x=n、y=−tを持つ。(2)
dをqで割った余りをrとすると、d=qu+rと表される。
d≧pqより、u≧pでなければならない。(1)と同様にして、(A)の中にrと等しいものが必ず存在するので、これをrnとする。
pn=qt+rn=qt+r
pn−d=(qt+r)−(qu+r)=q(t−u)
よって、pn+q(u−t)=d。
pn=qt+r≦pq≦d=qu+r
従って、u−t≧0。
よって、px+qy=dは正または0の整数解x=n、y=u−tを持つ。(2)の別証明
(B)より、pn+q(−t)=1。
px+qy=d、pnd+q(−td)=d
(px+qy)−{pnd+q(−td)}=0
p(x−nd)=−q(y+td)
ところが、p、qが互いに素であるから、x−ndはqの倍数でなければならない。x−nd=qkと表される。
このとき、y+td=p(x−nd)/q=pqk/q=pk。よって、x=nd+qk、y=−pk−td。
これが、x、yともに正または0となるには、
nd+qk≧0、−pk−td≧0
すなわち、−nd/q≦k≦−td/p ・・・(C)を同時に満たす整数kが存在することが必要かつ十分。(−td/p)−(−nd/q)=(pn−qt)d/(pq)=d/pq≧1
より、(C)を満たす整数kが必ず存在する。よって、px+qy=dはx、yともに正または0の整数解を持つ。