第２８問の解答

１．問題

図１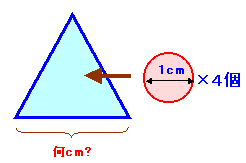

図２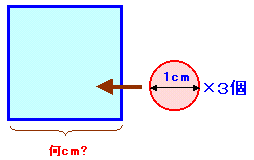

直径１ｃｍの硬貨があります。

（問１）この硬貨４枚を重ならないようにして正三角形の枠に収まるように配置します。
　　　　正三角形の一辺を出来るだけ小さくしたいのですが、最小で何ｃｍになるでしょうか？　　

（問２）正方形の枠に硬貨３枚を重ならないように配置する場合は、正方形の一辺は最小値何ｃｍ？

（注）答は、少数以下２桁まで求めて下さい。

２．解答例1

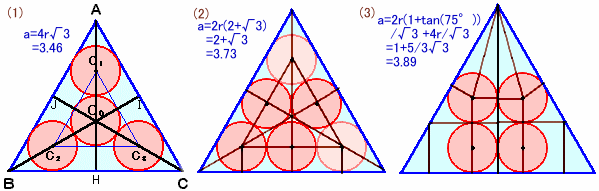
（問１）

上図（１）のように、真ん中に各辺と接しない硬貨がある場合が最も正三角形を小さくできます。
このとき、硬貨の半径をｒ、求める正三角形の１辺の長さをａとすると、
△ＢＣ₀Ｈは、１辺の長さが２ｒの正三角形のちょうど半分になるので、
　ＢＨ＝Ｃ₀Ｈ×√3=2r√3

よって、a=2BH=4r√3=2×1.732=3.46cmとなります。

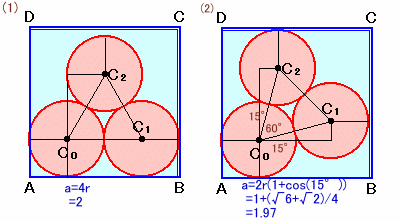
（問２）

３つの硬貨が接する形で、上図（１）の場合から反時計回りに回転していき、ちょうど対角線ＡＣに関して対象となる（２）の場合が最も正方形の１辺の長さａを小さくできます。

このとき、
　ａ＝２ｒ（１＋ｃｏｓ（１５°））
　　＝１＋（√６＋√２）／４
　　＝１．９７cm
となります。

　

答：（問１）３．４６cm（問２）１．９７cm

以上　　