第３０問の解答

---

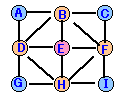
１．問題

左図のように９個のマスと、これらを結ぶ線分があります。 これらのマスを、駒が次のように移動するものとします。 　・最初、駒はＥにある。 　・駒が次に移動できるマスは、線分で結ばれた隣のマスのみであり、 　　そのうちどのマスに移動するかは同じ確率とする。 時間がかなり経過したとき、 　・駒がＡ、Ｃ、Ｇ、Ｉにある確率をＰ、 　・駒がＢ、Ｄ、Ｆ、Ｈにある確率をＱ、 　・駒がＥにある確率をＲ とするとき、Ｐ：Ｑ：Ｒを求めて下さい。

---

２．解答例1(カミナリ親父さん、ありっちさん、ｔａｒｏさん、清川育男さん、Ｅ管理室建築Ｇさん、他多数)

ｔ時点において、駒がＡ、Ｂ、Ｃ、・・・、Ｉにある確率をa_t、b_t、c_t、・・・、i_t、
Ａ、Ｃ、Ｇ、Ｉにある確率をＰ_t、Ｂ、Ｄ、Ｆ、Ｈにある確率をＱ_t、Ｅにある確率をＲ_tとします。

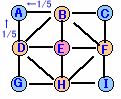
図１	at+1＝1/5・bt+1/5・dt　・・・（１） ct+1＝1/5・bt+1/5・ft　・・・（２） gt+1＝1/5・dt+1/5・ht　・・・（３） it+1＝1/5・ft+1/5・ht　・・・（４） Pt＝at+ct+gt+it　　　　・・・（５）
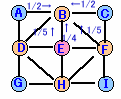
図２	bt+1＝1/2・at+1/2・ct+1/5・dt+1/5・ft+1/4・et　・・・（６） dt+1＝1/2・at+1/2・gt+1/5・bt+1/5・bt+1/4・et　・・・（７） ft+1＝1/2・ct+1/2・it+1/5・bt+1/5・ht+1/4・et　・・・（８） ht+1＝1/2・gt+1/2・it+1/5・dt+1/5・ft+1/4・et　・・・（９） Qt＝bt+dt+ft+ht　　　・・・（１０）
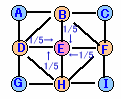
図３	et+1＝1/5・bt+1/5・dt+1/5・ft+1/5・ht　・・・（１１） Rt＝et　・・・（１２）

（１）〜（５）より、
P_t+1＝a_t+1+c_t+1+g_t+1+i_t+1
　　　＝（1/5・b_t+1/5・d_t）+（1/5・b_t+1/5・f_t)+(1/5・d_t+1/5・h_t)+(1/5・f_t+1/5・h_t)
　　　＝2/5・(b_t+d_t+f_t+h_t)
　　　＝2/5・Ｑ_t　　・・・（１３）

（６）〜（１０）より、
Q_t+1＝b_t+1+d_t+1+f_t+1+h_t+1
　　　＝（1/2・a_t+1/2・c_t+1/5・d_t+1/5・f_t+1/4・e_t）
　　　　+（1/2・a_t+1/2・g_t+1/5・b_t+1/5・b_t+1/4・e_t)
　　　　+(1/2・c_t+1/2・i_t+1/5・b_t+1/5・h_t+1/4・e_t)
　　　　+(1/2・g_t+1/2・i_t+1/5・d_t+1/5・f_t+1/4・e_t)
　　　＝(a_t+c_t+d_t+i_t)+2/5・(b_t+d_t+f_t+h_t)+e_t
　　　＝P_t+2/5・Ｑ_t+R_t　・・・（１4）

（１１）、（１２）より、
R_t+1＝e_t+1
　　　＝（1/5・b_t+1/5・d_t+1/5・f_t+1/5・h_t)
　　　＝1/5・Ｑ_t　・・・（１５）

（１３）〜（１５）より、
Q_t+1＝P_t+2/5・Ｑ_t+R_t
　　　＝2/5・Ｑ_t-1＋2/5・Ｑ_t+1/5・Ｑ_t-1　
　　　＝2/5・Ｑ_t＋3/5・Ｑ_t-1　　・・・（１６）

この漸化式より、一般解Ｑ_tは、x²-2/5・x-3/5=0の根x=1、-3/5を用いて、
　　Ｑ_t＝A・1^t＋B・(-3/5)^tと表すことが出来ます。
ここで、Ｑ₀＝0、Ｑ₁＝１より、
　　A＋B＝0、A＋B・(-3/5)＝1を解いて、A=5/8、B=-5/8を得ます。
よって、
　　Ｑ_t＝5/8-5/8・(-3/5)^t　・・・（１７）
となります。

（１３）、（１５）より、
　P_t＝2/5・Q_t-1＝1/4-1/4・(-3/5)^t-1　・・・（１８）
　R_t＝1/5・Q_t-1＝1/8-1/8・(-3/5)^t-1　・・・（１９）

よって、t→∞のとき、P_t→2/8、Q_t→5/8、R_t→1/8。
従って、P=2/8、Q=5/8、R=1/8。
　　P：Q：R=２：５：１　となります。

答：２：５：１

以上　　

---