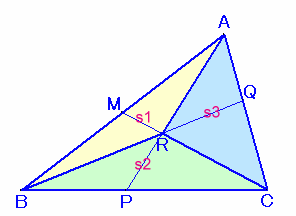
（チェバの定理）
Rを三角形の内部の点とし、ARの延長と辺BCの交点をP、ARの延長と
辺BCの交点をP、BQの延長と辺CAの交点をQ、CRの延長と辺ABの
交点をMとすると、次式が成り立つ。

　参考図１
(AM/MB)・(BP/PC)・(CQ/QA)＝１

（証明）
s1＝△ABR、s2＝△BCR、s3＝△CARとします。
△ABP：△APC＝△RBP：△RPC＝BP：PC。
よって、s1：s3＝(△ABP−△RBP)：(△APC−△RPC)＝BP：PC。
　　・・・　（１）

同様に、
　s2：s1＝CQ：QA ・・・　（２）、　s3：s2＝AM：MB ・・・　（３）

（３）×（１）×（２）より、
　(AM/MB)・(BP/PC)・(CQ/QA)＝(s3/s2)・(s3/s2)・(s3/s2)＝１

 （補題）
左図で、次式が成り立つ。
　AR/RP＝QA/CQ＋AM/MB、
　BR/RQ＝MB/AM＋BP/PC、
　CR/RM＝PC/BP＋CQ/QA

（証明）
　AR/RP＝△ABR/△RBP＝s1/(s2×BP/BC)、
　AR/RP＝△ARC/△RPC＝s3/(s2×PC/BC)。

よって、
　(AR/RP)×(BP/BC)＋(AR/RP)×(PC/BC)
　　＝s1/s2＋s3/s2
従って、
　AR/RP
＝s1/s2＋s3/s2
＝QA/CQ＋AM/MB

他も同様。