ピックの定理

（証明）

Pが格子多角形（頂点が全て格子点）のとき、
　Pの面積をA（P)
　F（P)＝１/２×B(P)＋I(P)−１
と表すこととします。

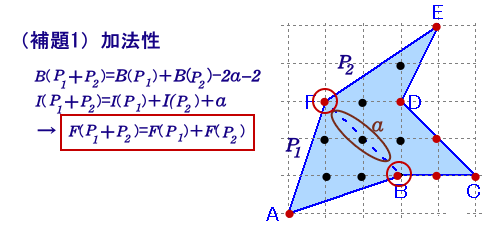
（補題１）F(P)は、加法性がある。
すなわち、格子多角形Pが２つの格子多角形P1とP2に分割されるとき、
P＝P1＋P2のように書くとすると、
　F（P1＋P2）＝F(P1）＋F（P2）
　F（P1−P2）＝F(P1）−F（P2）
が成り立つ。

参考図１

（証明）
P1とP2の共通部分でPの内部にある格子点数をaとすると、
 B（P1＋P2)＝B(P1）＋B（P2）-2a-2
I（P1＋P2)＝I(P1）＋I（P2） ＋a
よって、
　F（P1＋P2)
＝１/２×B（P1＋P2)＋I（P1＋P2)-1
＝１/２×｛B(P1）＋B（P2）-2a-2｝＋｛I(P1）＋I（P2） ＋a｝−１
＝｛１/２×B(P1）＋I(P1）−１｝＋｛１/２×B(P1）＋I(P1） −１｝
＝F（P1)＋F（P2)

従って、
　F（P1）＝F（（P1−P2)＋P2）＝F（P1−P2)＋F(P2）
よって、
　F（P1−P2)＝F（P1）−F(P2）

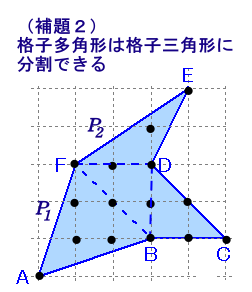
（補題２）任意の格子多角形は、格子三角形に分割できる。

参考図２

（証明）
任意の多角形は三角形に分割することができる（証明略）ので明らか。

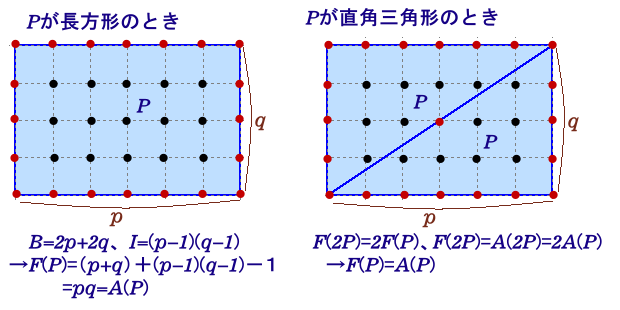
（補題３）任意の格子直角形、格子直角三角形についてピックの定理が成り立つ。

参考図３

（証明）
まず、格子長方形Pの場合、横の長さをp、縦の長さをqとします。
B＝2p＋2q、I＝(p-1)(q-1)より、
F（P)＝１/２×（2p＋2q）＋(p-1)(q-1)−１＝pq＝A（P)
よって、ピックの定理が成り立ちます。

次に、直角三角形Pの場合、補題１より、F（２P）＝２F（P)
また、２Pは長方形だから、F（２P)＝A(２P）＝２A(P)
よって、F（P）＝A(P)となり定理が成り立つ。

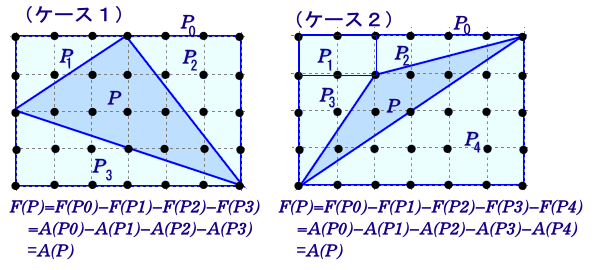
（補題４）任意の格子三角形についてピックの定理が成り立つ。

参考図４

（証明）
格子三角形Pに外接する格子長方形をP0とすると、
ケース１では、P＝P0-P1-P2-P3だから、補題１より、
F(P)＝F(P0-P1-P2-P3)
　　＝F(P0)−F(P1)−F(P2)−F(P3)
　　＝A(P0)−A(P1)−A(P2)−A(P3)　←補題３
　　＝A（P)
となり、Pについても定理が成り立つ。

さて、任意の格子多角形Pは補題２より、格子三角形P１、P2、・・・、Pnに分割されます。
補題１の加法性より、
F（P）＝F（P1＋P2＋・・・＋Pn）
　　　＝F(P1)＋F(P2)＋・・・＋F(Pn)
　　＝A(P1)＋A(P2)＋・・・＋A(Pn)　←補題４
　　＝A（P)
となり、Pについて定理が成り立つ。