第１５６問の解答

１．問題　［空間図形］

問題図

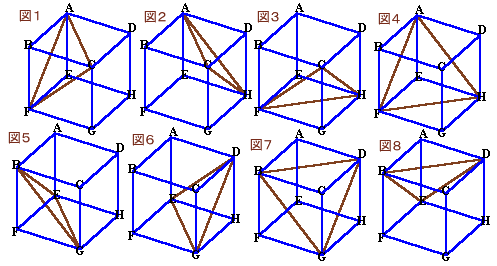
一辺の長さが５cmの立方体があります。
　この立方体を、上の図のような方法で８回切断します。

　このとき、８回の切断が終わるまで立方体は動かしません。つまり、８回の切断が終了するまでは、この立体は立方体の形を保っており、切断が終了するとバラバラになるというわけです。

　さて、この作業後にできた、たくさんの小さな立体のうち最も体積が大きい立体は何cm3でしょうか。

２．解答例１(ｋｕｒｉ他多数)

第１３１回問題が参考になります。

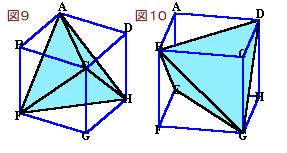
最初の４回の切断（図１〜図４）で図９のような正４面体が、またあとの４回の切断（図５〜図８）のみでは図１０のような正四面体ができます。

参考図１

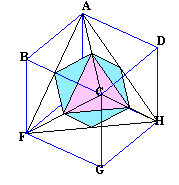
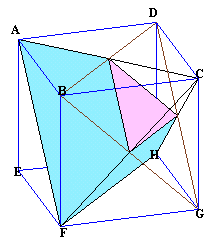
これらの共通部分として下図のような正八面体が残ります。

参考図２

さて立方体の体積をＶとし、図９の正四面体の体積をＶ１、正八面体の体積をＶ２とします。

最初の４回の切断では、１回の切断で立方体から各面が直角２等辺三角形の三角錐を切り取ることになるので、　
　Ｖ１＝Ｖ−（Ｖ×1/2×1/3）×４＝Ｖ×1/3

参考図３

次の切断では、Ｖ１から1/8ずつ切り取ることになるので、
　Ｖ２＝Ｖ１−（Ｖ１×1/8）×４＝Ｖ１×1/2＝Ｖ×1/6＝１２５／６ｃｍ3

となります。

答：１２５／６ｃｍ3

以上