第１７６問の解答　設問（２）

１．問題　［空間図形］　設問（２）

問題図2
（２）　さて、正四面体ＡＢＣＤの全ての辺をそれぞれ両方向に２倍ずつ伸ばすと、全部で１２個の点ができます。これらの１２個の点を頂点とする立体（凸多角形）の体積は、もとの正四面体の体積の何倍でしょうか。

（注１）左図は、例として辺ＡＢを両方向に２倍ずつ伸ばしてＥ、Ｆをとったところを示しています。当然ＥＦ＝ＡＢ×３です。

　

２．解答例０

まず、求める立体がどんな形になるかを考えましょう。

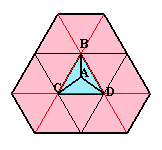
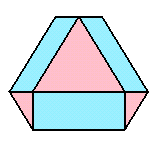
底面ＢＣＤの各辺（長さを１とします）を伸ばしてみます。

底面ＢＣＤ
底面ＢＣＤ		 全体図
全体図

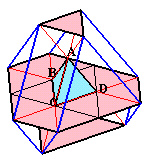
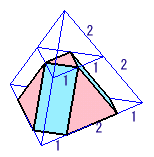
底面ＢＣＤである正三角形を１２個集めた形になります。

同様に、ＡＢ、ＡＣ、ＡＤを伸ばしてみると、

からなることが分かります。

これを、各方向から見た図を見てみましょう。

平面図（上から見た）
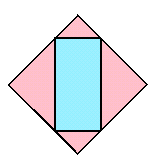
平面図		 側面図（右から見た）
側面図		 （参考）マウスでドラッグして下さい。
立面図（前から見た）
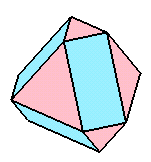
立面図		 俯瞰図（斜め上から）
俯瞰図

３．解答例１（CRYING DOLPHINさん、中村明海さん他）

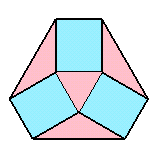
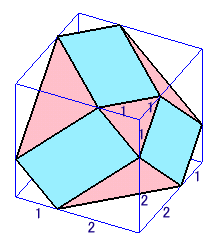
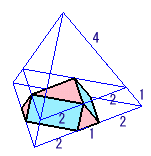
６個の長方形が実は互いに直交していることが分かります。

参考図9

そこで、下図のように各長方形を面に含むような立方体を考えると、求める立体がこの立方体の各辺を１：２に分ける点を頂点としていることが分かります。

参考図10 （参考）マウスでドラッグして下さい。

よって、この立方体の辺の長さは、元の正四面体（V0）がすっぽり入る立方体の辺の長さの３倍になっていることになります。

元の立方体の１辺の長さを１とします。
大きい立方体の体積＝３3＝２７=V0×８１

大きい立方体から切り取る、
　小さい三角錘の体積＝1/3×（1/2×１2）×１＝1/6＝Ｖ０×1/2
　大きい三角錘の体積＝1/3×（1/2×２2）×２＝4/3＝Ｖ０×４

よって、求める立体の体積
　＝V0×８１−（Ｖ０×1/2＋Ｖ０×４）×４
　＝V0×８１−V0×１８
　＝V0×６３

従って、求める立体の体積は元の正四面体の体積の６３倍となります。

答：６３倍

４．解答例２（長野　美光さん）

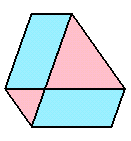
底面ＢＣＤより上側と下側で２つに分解し、下側は、見やすくするために逆さにします。

上側
参考図11		 下側
参考図12

元の正四面体の大きさを１（辺の長さ、高さ、面積、体積すべて１とみなす） とすると、 

上側：
　１辺４の正四面体（体積６４）の１つの頂点から１辺２の正四面体（体積８）を 
切り取り、さらに底面積１、高さ２の三角柱（体積６）を３つ切り取りとる
　体積＝６４−８−３×６＝３８

下側：
　１辺５の正四面体（体積１２５）の１つの頂点から１辺４の正四面体（体積６４）を 
切り取り、さらに底面積４、高さ１の三角柱（体積１２）を３つ切り取る
　体積＝１２５−６４−３×１２＝２５ 
 
になります。

従って、求める体積は、３８＋２５＝６３　となります。　

５．解答例３（わかさひ君、中学への算数学コンさん、マサルさん他）

問題の立体の各面に対し、元の正四面体の頂点のうち近いものとを結んでできる立体を考える。

参考図13

よって、合計＝1×４＋７×４＋５×６＋１＝６３ となります。

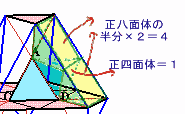
なお、長方形に対応する立体は、長方形を２分すると、
　正八面体の半分×２個＝正八面体（体積４）（設問１からの誘導）と
　正四面体（体積１）
に分かれるので、合計体積＝５と求めることも出来ます。

参考図14

［設問１へ］