第176問の解答 設問(1)
1.問題 [空間図形] 設問(1)
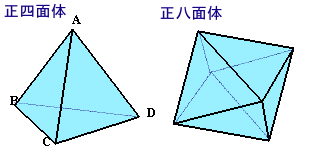
| (1) 一辺の長さが2cmの正四面体は、一辺の長さが1cmの正四面体(ア)個と、 一辺の長さが1cmの正八面体(イ)個でできています。 ア、イに当てはまる整数を答えてください。 |
2.解答例
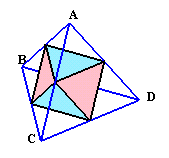
下図のように、正四面体の各辺の中点を結んでできる立体は、正八面体になります。
(参考)マウスでドラッグして下さい。
大きい正四面体(辺の長さ2cm)は、正八面体(辺の長さ1cm)1個と各頂点の部分に残る小さい正四面体(辺の長さ1cm)4個に分かれます。
答え:(ア)4個 (イ)1個
3.参考
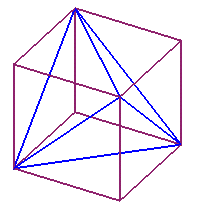
立方体の対角線を下図のように結ぶと正四面体ができます。
(参考)マウスでドラッグして下さい。
この、正四面体の体積と立方体の体積比を求めてみましょう
立方体の1辺の長さを1とします。
立方体の体積=13=1各頂点にある三角錘の体積=1/3×(1/2×12)×1=1/6
よって、正四面体の体積=1−1/6×4=1/3
従って、正四面体の体積:立方体の体積=1:3となります。
[設問2へ]