第180問の解答
1.問題 [場合の数]
| マサルさんの経営する店は、1個50円の商品だけを売っている「50円ショップ」です。 ある朝、開店してみると、50円玉が1枚もないことに気づきました。これではおつりを出すことが出来ません。 結局この日は、50円玉しか持っていない人と100円玉しか持っていない人が同数だけ来たのですが、うまい具合にお客さんが来てくれたので、100円玉しか持っていない人に「おつりがないからお断り」はしないで済んだそうです。 このとき、例えば全部で4人のお客さんが来店したとすると、マサルさんの硬貨の受け取り方は、 A.50円玉→ 50円玉→100円玉→100円玉 B.50円玉→100円玉→ 50円玉→100円玉 の2通りが考えられますね。 さて、全部で10人のお客さんが来たとすると、マサルさんの硬貨の受け取り方は何通り考えられるでしょうか。 注・・・1人のお客さんは1個の商品だけを買うものとします。また、50円玉、100円玉以外の硬貨・紙幣は全く持ってないものとします。 |
2.解答例1(うつさん、南の源さん他多数)
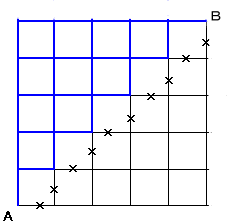
50円玉しか持っていない人が来ることをN、100円玉しか持っていない人が来ることをEと表すことにすると、題意を満たす受け取り方は、下図のような5×5の格子上を北に進むことをN、東に進むことをEと表したときの、最短経路と対応する。
ただし、「どの格子点でもそれまでのEの個数よりNの個数のほうが多い」ことが条件になるので、「×印より右下方向へは進めない」ことになります。
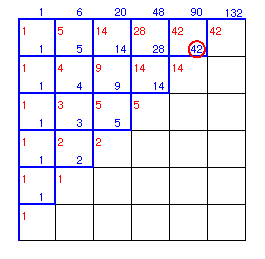
最短経路の個数は、下図のように、各格子点について南から来る経路と西から来る経路の和となるので、A地点から順次計算していけば良いことになる。
従って、求める最短経路の個数は42個なので、求める硬貨の受け取り方も42通りとなる。
答:42通り
以上
3.解答例2(あれふさん、Tak'Sakaiさん、清川育男さん他多数)
題意を満たす場合の数は、カタラン数と呼ばれ、
K(5)
=2・5C5/(5+1)
=(10・9・8・7・6/5・4・3・2・1)/6
=42通り
で求められる。なお、カタラン数については算チャレ1、2や私の「算数チャレジャーに挑戦第6問」等にも出たことがあります。