第２０３問の解答

---

１．問題　［立体図形］

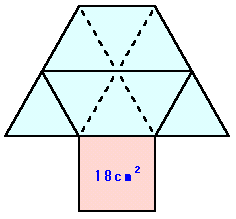
左図は、ある立体の展開図で、ピンク色の正方形の面積が１８cm2となっています。水色の台形部分は、正方形と一辺の長さが等しい正三角形８つでできており、実線部分を折り曲げて立体を作ります。 　では、この展開図を組み立てて出来る立体の体積は何cm3でしょうか。

---

２．解答例１（Hamayanさん、CRYING DOLPHINさん、Gouさん、祝いビルさん、おがけんさん、トトロ＠Ｎさん、長野美光さん、中村明海さん、他多数）

問題の立体は図１のようになります。
これを２個、底面同士をくっつけて片方を９０度ひねると図２のように正四面体ができます。

（参考）JavaAppletによる動く立体図

図１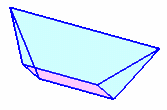 図２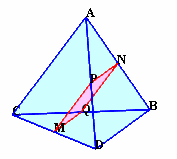

図３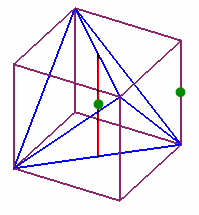

図４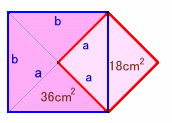 図５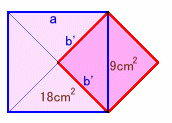

図３から、正四面体の体積は、立方体から４個の三角錐を取り除いたものと等しいことから、立方体の体積の１/３となります。（第１７６問、第１３１問参照）

図１で底面である正方形の一辺の長さをaとすると、a²＝１８。
図２で正四面体の一辺の長さは、2a。
図３で立方体の一辺の長さをbとすると、b²＝2a²=36、
　よってb=6。（図４を参照）

求める立体の体積をＶとすると、2V=b³×1/3、Ｖ＝b³/6＝6³/6=36となります。

答：３６ｃｍ³

　以上

---

３．解答例２（ありっちさん、M.Hossieさん、うっしーさん、他）

下図に求める立体を３つの部分に切断すると、真ん中は三角柱、両端の三角錐を合わせると一辺の長さがａの正四面体ができます。

正四面体の体積をＶ_１、真ん中の三角柱の体積をＶ_２とすると、合わさった部分の三角形は共通だから、Ｖ_１/２＝（Ｖ_２/２）/３、Ｖ_１＝Ｖ_２/３、
よって求める立体の体積Ｖ＝Ｖ_１＋Ｖ_２＝Ｖ_１×４。

解答例１の図３と同様に正四面体がすっぽり入る立方体（一辺の長さb'）を考えると、b'²=a²/２=９、よってb'=3。（図５参照）
従って、V=b'³/３×４=３³/３×４＝３６。

　以上

４．解答例３（H.Takaiさん他）

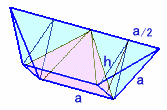
上図のように、一辺がａの正四面体２個と、一辺がａの正方形を底面とする四角錐に分かれます。

正四面体の体積は、解答例２と同様にして、３³/３＝９cm³。

四角錐の高さは、正四面体の相対する二辺の距離だから、図３より正四面体をすっぽり包む立方体の一辺すなわちb'=３ｃｍ。

よって、四角錐の体積＝１/３×１８×３＝１８cm³。

以上から、求める立体の体積＝９×２＋１８＝３６cm³。