第211問の解答
1.問題 [平面図形]
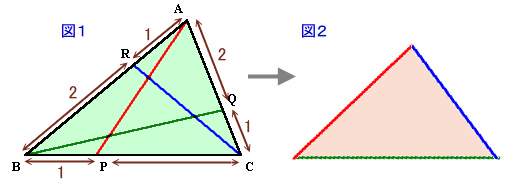
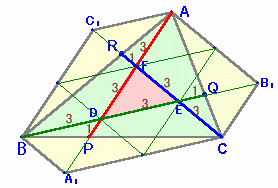
| 上の図のような三角形ABCがあり、その面積は36cm2です。 いま、辺ABを1:2に分ける点をR、辺BCを1:2に分ける点をP、辺CAを1:2に分ける点をQとし ます。 さて、AP、BQ、CRを結び、それら(AP、BQ、CR)を3辺とする三角形を作るとき(図2参 照)、その面積は何cm2でしょうか? |
2.解答例1(たなかさん、あすとさん、長野美光さん、萬田銀次郎さん、他多数)
「算数チャレンジャーに挑戦」第29問に類題があります。
真ん中の三角形をDEFとすると、△DEF=△ABC×1/7。
AP:FD=BQ:DE=CR:EF=7:3。よって、求める三角形の面積
=△DEF×(7/3)2
=△ABC×1/7×49/9
=36×7/9
=28cm2。
答:28cm2
以上
3.解答例2(ヒデー王子さん、糸瀬善人さん、他)
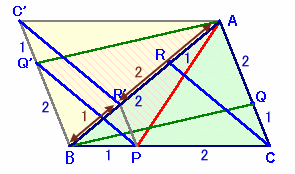
△ABCを回転移動し辺ABの上にくっつけて 、平行四辺形AC'BCを作ります。
Q、Rが動いた点をQ'、R'とすると、BQ':Q'C'=2:1、AR':R'B=2:1。AQ=BQ'でAQ//BQ'より、AQ'BQも平行四辺形、よってAQ'=BQ。
BR':R'A=BP:PC=2:1より、R'P//AC、R'P=AC×1/3。
BC//ACより、C'Q'//R'P、C'Q'=BC'×1/3=R'P。 ・・・(1)従って、CQ'PR'も平行四辺形、よってQ'P=C'R'。
△BC'R'は△ACRを回転させたものだから、C'R'=CR。 ・・・(2)
よって、Q'P=CR。以上から、求める三角形は△APQ'と合同。
△ABC=Sとおくと、
△APQ'=平行四辺形AC'BC−(△AQ'C'+△APC+△PBQ')
=S×2−(S×1/3+S×2/3+S×1/3×2/3)
=S×7/9
=28cm2。
4.解答例3(H.Takaiさん、うっしーさん、他)
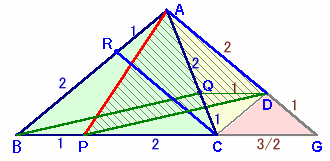
AからRCに平行に引いた直線とBCの延長との交点をGとし、
QからBGに引いた直線とAGとの交点をDとします。
RC//AGより、BR:RA=BC:CG=2:1。
よって、CG=BC×1/2。AG=RC×3/2。QD//CGより、AQ:QC=AD:DG=2:1、
AD=AG×2/3=RC×3/2×2/3=RC。 ・・・(1)QD=CG×2/3=BC×1/2×2/3=BC×1/3=BP。
BP//QDだから、BPDQは平行四辺形となり、BQ=PD。 ・・・(2)以上より、求める三角形と△APDは合同。
S=△ABCとおくと、
△APG=△APC+△ACG=S×2/3+S×1/2=S×7/6。
△APD=△APG×2/3=S×7/6×2/3=S×7/9=28cm2。
5.解答例4(dragon-kさん、他)
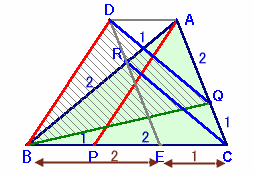
AからPAに平行に引いた直線とAからBCに平行に引いた直線の交点をDとし、BCを2:1に内分する点をEとします。
DA//BP、DB//APより、DBPAは平行四辺形。
よって、DB=AP、DA=BP。 ・・・(1)DA//ECで、EC=BC×1/3=BP=DA。
よって、DECAは平行四辺形となり、DE=AC。DA//BEより△ADR∽△BRE、
よって、DR:RE=DA:BE=EC:BE=1:2。従って、DR=DE×1/3=AC×1/3=QC。
DR//QC、DR=QCより、DRCQは平行四辺形。
よって、DQ=RC。 ・・・(2)以上より、求める三角形と△DBQは合同。
△DBQ=台形DBCA−(△QBC+△DAQ)
台形DBCA=△ABC+△ABD=S+S×1/3=S×4/3。
△QBC=S×1/3。
△DAQ=△ADC×2/3=△AEC×2/3
=S×1/3×2/3=S×2/9。よって、△DBQ=S×4/3−S×1/3−S×2/9=S×7/9=28cm2。