第２１２問の解答

---

１．問題　［場合の数］

Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆさんの６人の名札があり、それぞれ中が見えない６つの袋の中に入っています。 　いま、Ａ〜Ｆさんの６人がそれぞれ１つの袋を選んで名札を取り出すとき、６人とも他人の名札に当たる場合は何通りありますか。

（参考）「算数チャレンジャーに挑戦」第７問に類題があります。

---

２．解答例１（たなかさん、ＡЯＯＴさん、長野美光さん、すけさん、あまれっとさん、あんみつさん、他多数）

円順列（巡回順列）のパターンで場合分けします。
なお、Ａ、Ｂ、・・、Ｆの替わりに番号１、２、・・、６で表すことにします。

・６個の円順列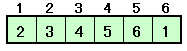 　 　５!=5×４×３×２×１＝１２０通り	・４個の巡回順列＋２個の円順列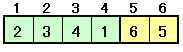 　 　6C4×3!×1!=15×6×1＝９０通り
・３個の巡回順列＋３個の円順列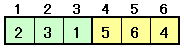 　 　6C3/2×２!×２!=20/2×2×2＝４０通り	・２個の巡回順列＋２個の円順列＋２個の円順列 　 　6C2×4C2/3!×1!×1!×１! =15×6/6＝１５通り

合計１２０＋９０＋４０＋１５＝２６５通り

答２６５通り

　以上

---

３．解答例２
（萬田銀次郎さん、ταροさん、杉本未来さん、きょえぴさん、さとけんさん、ヒデー王子さん、出口さん、他多数）

袋、名札の個数がｎのとき袋と名札の番号が全て異なる場合の数をａ_nで表し、ａ_nに関する漸化式を考えます。

１番目の袋には、ｍ番目の名札（m≠1）の（n-1）通り。

（ア）１番目の札がｍ番目の袋に当たるとき

１、ｍ番目を除くと、（n-2）個の袋、名札数で番号が異なる場合に該当するので、ａ_n-2通り。
よって、合計(n-1)×ａ_n-2通りになります。

（イ）１番目の札がｍ番目以外の袋に当たるとき

１番目を除くと、（n-1）個の袋、人数で番号が異なる場合に該当するので、ａ_n-1通り。
よって、合計(n-1)×ａ_n-1通りになります。

（ア）、（イ）より、
　　ａ_n＝(n-1)｛ａ_n-2＋ａ_n-1｝　　・・・　（１）
となります。

ａ₁＝0、ａ₂＝1、より、（１）の漸化式を用いてａ_nを順次求めると、

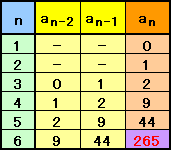
ａ₃＝2、ａ₄＝9、ａ₅＝44、ａ₆＝265　を得ます。 

---

４．解答例３（ヒデー王子さん、B2さん、他）

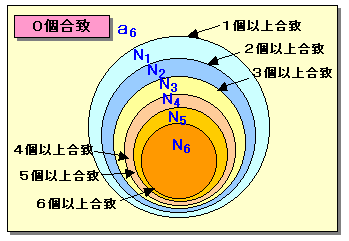
ｎ個の袋、名札で全ての入れ方をＮ 、
袋と名札の番号が、少なくともm個は一致する入れ方をＮ_mなどとあらわすことにします。

組み合わせの包除原理により、全ての袋と名札の番号が異なる入れ方ａ_nは、重複して引いてしまう部分を差し引きしていくと、
　ａ_n＝Ｎ−Ｎ_１＋Ｎ_２−Ｎ_３＋Ｎ_４−・・・・ ＋(-1)ⁿＮ_n
となります。

Ｎ＝ｎ!、および
Ｎ_mについては、一致する１枚の選び方がnＣm通り、残りの並べ方が（n-m）!通りなので、Ｎ_m＝_nＣ_m×（n-m）!＝n!/m!通り。
従って、
　ａ_n＝n!−n!＋n!/2!−n!/3!＋n!/4!−・・・・ ＋(-1)ⁿn!/n!
　　　＝n!/2!−n!/3!＋n!/4!−・・・・ ＋(-1)ⁿn!/n!　　・・・（２）
となります。　　 
本問では　　　　　　　　　　　　　　　　　　 
 ａ₆＝6!−6!＋6!/2!−6!/3!＋6!/4!−6!/5!+6!/6!
　　＝360-120+30-6+1
　　＝265 通り。 

（参考）漸化式（１）より、一般式（２）を得る方法

（１）より、b_n＝ａ_n/n!とおくと、
n!b_n＝(n-1)｛(n-2)!b_n-2＋(n-1)!b_n-1｝
n!b_n＝(n-1)!b_n-2＋(n-1)(n-1)!b_n-1
nb_n＝b_n-2＋(n-1)b_n-1
n(b_n−b_n-1)＝−（b_n-1−b_n-2)
b_n−b_n-1＝−(b_n-1−b_n-2)/n
　　＝（−１）²(b_n-2−b_n-3)/n・(n-1)＝・・・
　　＝（−１）^n-2(b₂−b₁)/n・(n-1)・・3
　　＝（−１）ⁿ(1/2!−0/1!)/n・(n-1)・・3
　　＝（−１）ⁿ/n!

よって、
　b_n＝b₁+Σ_k=2..n（b_k−b_k-1）
　　　＝Σ_k=2..n（−１）^k/k!
　　　＝1/2!−1/3!＋1/4!−・・・・ ＋(-1)ⁿ/n!
従って、　
　　ａ_n＝n!/2!−n!/3!＋n!/4!−・・・・ ＋(-1)ⁿn!/n!

さて、b_nは、全ての袋と名札の番号が異なる確率となるが、
n→∞のとき、b_n＝1/2!−1/3!＋1/4!−・・・・ ＋(-1)ⁿ/n!→1/e
となります。
なんとならば、e^xのマクローリン展開により、
　e^x＝lim_n→∞{1+x/1!+x²/2!+x³/3!＋x⁴/4!＋・・・・ ＋xⁿ/n!}
x=-1を代入すると、
　e^-1＝lim_n→∞{1-1/1!+1/2!-1/3!＋4/4!＋・・・・ ＋(-1)ⁿ/n!}

(中村明海さん、武田浩紀さん、まるケンさん）

---