第220問の解答
1.問題 [空間図形]
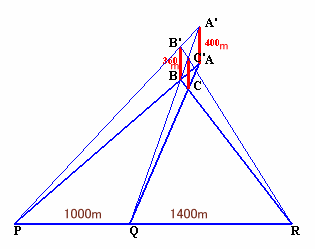
| ある町には、3本の煙突A、B、Cがたっているそうです。 煙突Aは高さ400m、煙突Bは高さ360mで、煙突Cは煙突A、Bよりも低いそうです。 いま、P地点からは、煙突Aの先端と煙突Bの先端がちょうど重なって見えたそうです。 また、Q地点からは、煙突Aと煙突Cの先端が、R地点からは煙突Bと煙突Cの先端が ちょうど重なって見えました。 P地点とQ地点は1000m離れており、Q地点とR地点は1400m離れているそうです。 では、煙突Cの高さは何mでしょうか。 (注意) 煙突A、B、CおよびP地点、Q地点、R地点は同一の平らな地面の上にあるものと します。 |
2.解答例1(うっしーさん、DrKさん、KINさん、noetherさん、dragon-kさん、M.Hossieさん、航介さん、他多数)
煙突A、B、Cの先端をA’、B’、C’とします。
図1
図2
三角形A’B’C’を含む平面と地面(三角形ABCを含む平面) の交わりは直線になります。
P、Q、R とも、両方の平面に含まれるので、その交線上にあります。図1で、△A’APと△B’BPは相似だから、
AP:BP=400:360=10:9、
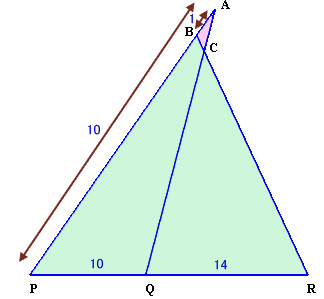
よって、AP:AB=A’P:A’B’=10:1 ・・・ (1)。図2で、△BPRと直線AQに関して、メネラウスの定理より、
BA/AP・PQ/QR・RC/CB=1
1/10・10/14・RC/CB=1
よって、RC:CB=14:1。図1で、△B’BRと△C’CRは相似だから、
B’B:CC=BR:CR=15:14、
よって、C’C=360×14/15=336mとなります。答 336m
以上
3.解答例2(トトロ@Nさん、萬田銀次郎さん、他)
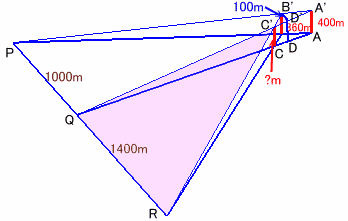
煙突A、B、Cの先端をA’、B’、C’とします。
解答例1と同様にして、P、Q、Rは一直線上にあります。
B’からPRに平行に直線を引き、A’Qとの交点をD’、その足下をDとします。
PQとB’D’が平行だから、三角形A’PQとA’B’D’は相似。
(1)より、PQ:B’D’=A’P:A’B’=A’Q:A’D’=10:1。 ・・・ (2)
よって、
B’D’=PQ×1/10=100m、
D’D=A’A×9/10=360m。 ・・・ (3)また、QRとB’D’が平行だから、三角形C’QRとC’D’B’は相似。
QC’:C’D’=QR:B’D’=14:1、
よって、
C’C=D’D×C’D’/QD’=360×14/15=336m。