第２２５問の解答

---

１．問題　［空間図形］

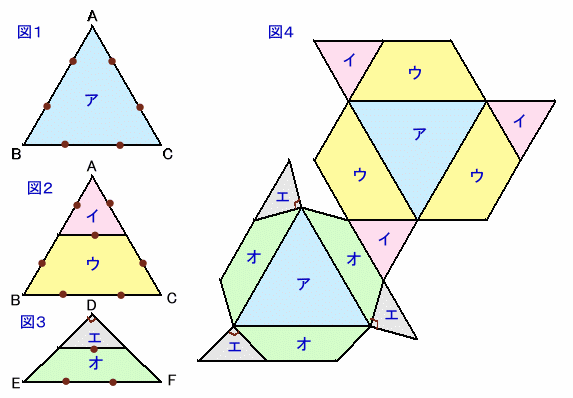
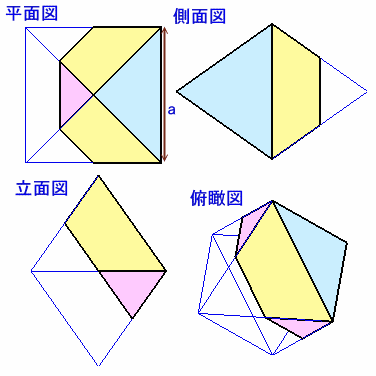
上の図４はある立体の展開図で、図１〜３で示されたア〜オの部品を使って作られています。この立体の体積は何cm3でしょうか。ただし、以下のような条件になっています。 図１の三角形ＡＢＣは正三角形 図２は三角形ＡＢＣの辺ＡＢ、ＡＣの中点をそれぞれＭ、Ｎとしてそれを結んだもの、 図３は斜辺の長さが図１の正三角形ＡＢＣの一辺と等しい直角二等辺三角形ＤＥＦを作り、 さらに長さが図２のＭＮと等しくなるようにＥＦの平行線ＰＱをひいたもので、ＤＥ＝１cmとなっています。

---

２．解答例１（ありっちさん、わかさひ君たーぼさん、M.Hossieさん、せんださん、mhayashiさん、他）

正三角形ＡＢＣの１辺の長さをaとします。
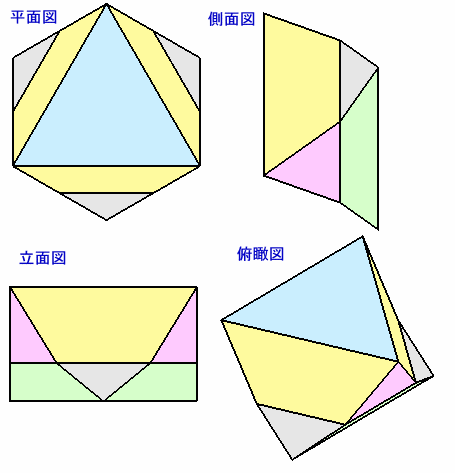
題意より、ＤＥ＝a/√2＝１、よってa＝√２。

さて、求める立体は下図のようになります。

真ん中にできた１辺a/2の正六角形で２つの立体に切断します。

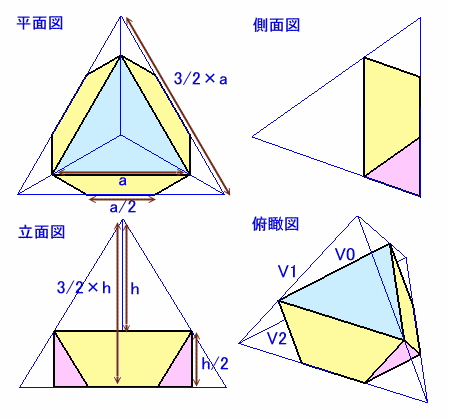
上側の立体（体積をV1とします）は、下図のように１辺3/2×aの正四面体から、１辺aの正四面体を１個、１辺a/2の正四面体を３個取り除いたものになります。

１辺aの正四面体の体積をＶ0とすると、
ｈ＝√（a²−（√3/3a）²）＝√6/3a。
V0＝1/3×｛1/2×a×√3/2a｝×√6/3a
　　＝√2/12×a³。

Ｖ１＝Ｖ0×（3/2）³−Ｖ0−Ｖ0×（1/2）³×３
　　＝V0×２
　　＝√2/12×（√2）³×２
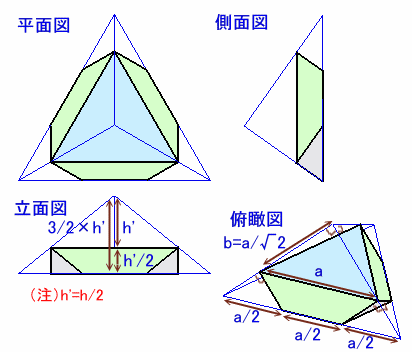
　　＝２/３cm³。

下側の立体（体積をV2とします）は、下図のように１辺3/2×aの正三角錐から、１辺aの正三角錐を１個、１辺a/2の正三角錐を３個取り除いたものになります。

１辺aの正三角錐の体積をＶ0'とすると、
ｈ'＝√（（√2/2a）²−（√3/3a）²）＝√6/6a＝h/2。
V0'＝1/3×｛1/2×a×√3/2a｝×√6/6a
　　＝√2/24×a³
　　＝V0/2。

Ｖ２＝Ｖ0'×（3/2）³−Ｖ0'−Ｖ0'×（1/2）³×３
　　＝V0'×２
　　＝Ｖ１／２
　　＝１/３cm³。

よって、求める立体の体積＝Ｖ１＋Ｖ２＝２/３＋１/３＝１cm³となります。

答：１cm³

---

３．解答例２（長野美光さん、ヒデー王子さん、C-Dさん、トトロ＠Ｎさん、あすとさん、あんみつさん、中村明海さん、糸瀬善人さん、H.Takaiさん、noetherさん、他）

上側の立体は、下図のように１辺aの正八面体を２等分したものに等しくなります。

１辺ａの正八面体の体積は、１辺aの正四面体の体積の４倍であり、
１辺aの正四面体の体積は、１辺bの立方体の体積の1/3となります。
（参考：第１７６回問題）

よって、Ｖ１＝1×1/3×４×1/2＝２/３cm³。

また下側の立体は、下図のように１辺bの立方体の半分から１辺aの正三角錐１個を除いたものに等しくなります。

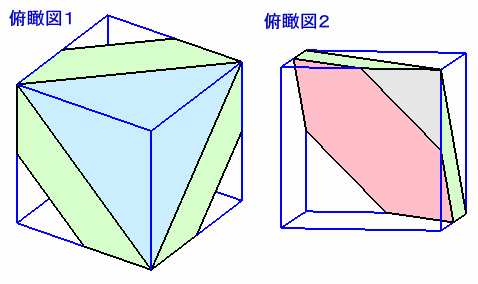
このうち、正三角錐の頂点は立方体の頂点にもなっていることから、
体積＝1/3×1/2b²×b＝1/6b³。

よって、Ｖ２＝b³×1/2−1/6b³＝1/6b³＝１/３cm³。

従って、求める立体の体積＝Ｖ１＋Ｖ２＝２/３＋１/３＝１cm³となります。