第２２９問の解答

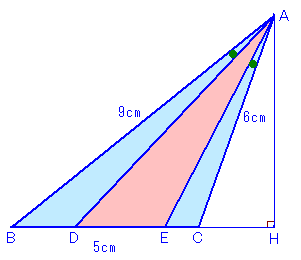
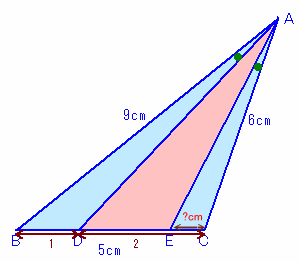
１．問題　［平面図形］

問題図
左図のような、　ＡＢ＝９cm、ＢＣ＝５cm、ＣＡ＝６cmの△ＡＢＣがあります。

いま、辺ＢＣ上にＢＤ：ＤＣ＝１：２となる点Ｄをとります。
さらに、∠ＢＡＤ＝∠ＣＡＥとなるような点Ｅをとります。

このとき、ＥＣの長さを求めてください。

２．解答例１（マサルさん、他）

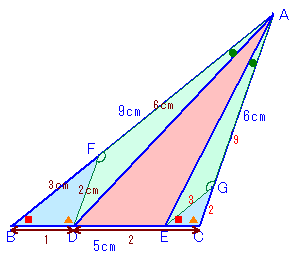
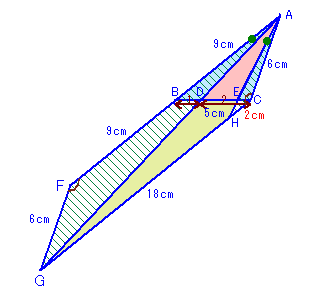
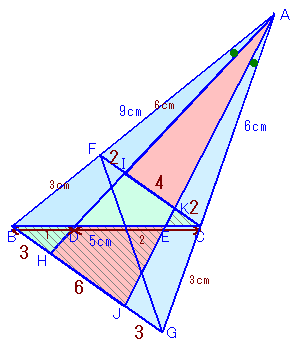
ＤからＣＡに平行に引いた直線とＢＡの交点をＦ、
ＥからＢＡに平行に引いた直線とＣＡの交点をＧ、
とします。参考図1

 ＦＤとＡＣが平行より、△ＦＢＤ∽△ＡＢＣで、
相似比はＢＤ：ＢＣ＝１：３。
よって、ＦＢ＝ＡＢ／３＝３ｃｍ、ＦＤ＝ＡＣ／３＝２ｃｍ。

ＡＢとＧＥが平行より、∠ＦＢＤ＝∠ＧＥＣ、
ＦＤとＡＣが平行より、∠ＦＤＢ＝∠ＧＣＥ。
よって、△ＦＢＤ∽△ＧＥＣ。
ＧＥ：ＧＣ＝ＦＢ：ＦＤ＝３：２。・・（１）

∠ＦＡＤ＝∠ＧＡＥ、∠ＡＦＤ＝∠ＡＧＥより、
△ＦＡＤ∽△ＧＡＥ。
よって、ＧＥ：ＡＧ＝ＦＤ：ＡＦ＝２：６＝３：９。・・（２）

（１）、（２）より、ＡＧ：ＧＣ＝９：２。

ＡＢとＧＥが平行より、△ＡＢＣ∽△ＧＥＣ。
よって、ＢＥ：ＥＣ＝ＡＧ：ＧＣ＝９：２。

従って、ＥＣ＝ＢＣ×２／１１＝５×２／１１＝１０／１１ｃｍ。


答：１０／１１ｃｍ

以上

３．解答例２（あやのりんさん、萬田銀次郎さん、ヒデー王子さん、トトロ＠Ｎさん、YokoyaMacさん、糸瀬善人さん、ありっちさん、長野美光さん、他多数）

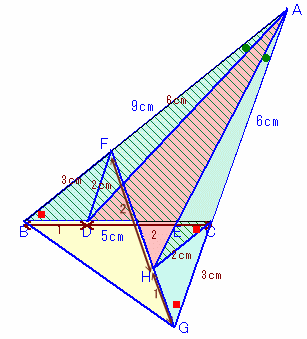
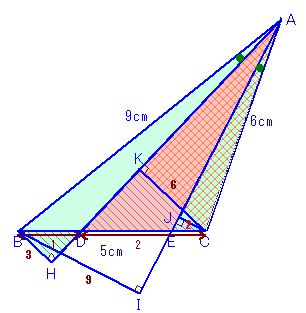
ＡＢ上にＡＦ＝６ｃｍとなる点Ｆを、
ＡＣの延長線上にＡＧ＝９ｃｍとなる点Ｇをとります。
また、ＡＥの延長線とＦＧの交点をＨとします。参考図2

 ＡＢ＝ＡＧ＝９ｃｍ、ＡＣ＝ＡＦ＝６ｃｍ、
∠ＢＡＧは共通より、△ＡＢＣ≡△ＡＧＦ。
よって、∠ＡＢＣ＝∠ＡＧＦ。

また、∠ＢＡＤ＝ＧＡＨ、ＡＢ＝ＡＧ。
よって、△ＡＢＤ≡△ＡＧＨ。
従って、ＢＤ＝ＧＨ、ＤＣ＝ＨＦ。

ＧＨ：ＨＦ＝１：２、ＧＣ：ＣＡ＝３：６＝１：２。
よって、△ＧＣＨ∽△ＧＡＦ。
従って、ＣＨ＝ＡＦ×１／３＝２ｃｍ。

ＣＨとＡＦが平行より、△ＣＦＥ∽△ＢＡＥ。
ＢＥ：ＥＣ＝ＡＢ：ＣＨ＝９：２。

従って、
ＥＣ＝ＢＣ×２／１１＝５×２／１１＝１０／１１ｃｍ。

４．解答例３（dragon-kさん、他）

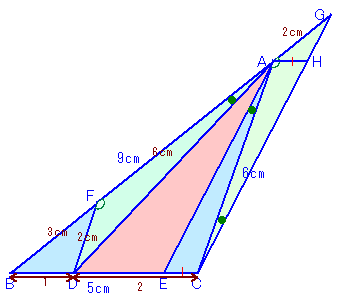
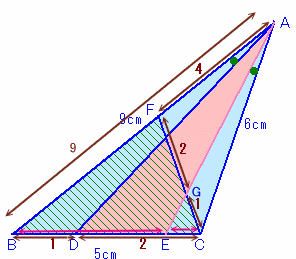
ＤからＡＣに平行線を引き、ＡＢとの交点をＦ、 
ＣからＡＥに平行線を引き、ＢＡの延長線との交点をＧ、
ＡからＢＣに平行線を引き、ＣＧとの交点をＨとします。 参考図3

 ＦＤとＡＣが平行より、△ＦＢＤ∽△ＡＢＣ。
ＦＢ＝ＡＢ×１／３＝３ｃｍ、ＡＦ＝６ｃｍ、
ＦＤ＝ＡＣ×１／３＝２ｃｍ。

ＡＥとＧＣは平行より、
∠ＡＣＧ＝∠ＣＡＥ＝∠ＦＡＤ、
ＦＤとＡＣが平行より、∠ＡＦＤ＝∠ＣＡＧ、
さらに、ＡＦ＝ＣＡ＝６ｃｍ、
よって、∠ＡＦＤ≡∠ＣＡＧ。
従って、ＡＧ＝ＦＤ＝２ｃｍ。

ＡＨとＢＣが平行より、△ＧＡＨ∽△ＧＢＣ。
ＡＨ：ＢＣ＝ＧＡ：ＧＢ＝２：１１。

よって、
ＡＨ＝ＢＣ×２／１１＝５×２／１１
　　＝１０／１１ｃｍ。

ＡＨとＥＣが平行、ＡＥとＨＣが平行より、
四角形ＡＥＣＨは平行四辺形。
よって、ＥＣ＝ＡＨ＝１０／１１ｃｍ。

５．解答例４（澪桜葵美翔さん、他）

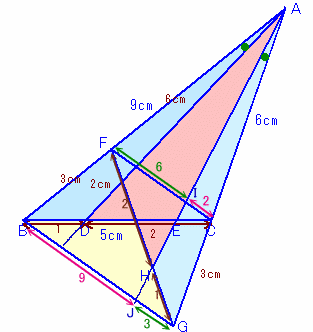
解答例２と同様に、ＡＢ上にＡＦ＝６ｃｍとなる点Ｆを、
ＡＣの延長線上にＡＧ＝９ｃｍとなる点Ｇをとります。
また、ＡＥの延長線とＦＧの交点をＨ、ＦＣとの交点をＩ、
ＢＧとの交点をＪとします。参考図4

 △ＡＦＣと△ＡＢＧは相似な二等辺三角形。
よって、ＦＣとＢＧは平行。

△ＡＩＣ∽△ＡＪＧ、
よって、ＩＣ：ＪＧ＝ＡＣ：ＡＧ＝６：９＝２：３。・・（１）

対象性より、ＧＨ：ＨＦ＝ＢＤ：ＤＣ＝１：２。
△ＨＪＧ∽ＨＩＦ、
よって、ＪＧ：ＦＩ＝１：２＝３：６。・・（２）

△ＡＦＩ∽△ＡＢＪ。
ＦＩ：ＢＪ＝ＡＦ：ＡＢ＝６：９。・・（３）

（１）、（２）、（３）より、ＩＣ：ＢＪ＝２：９。

△ＩＣＥ∽△ＪＢＥ、
よって、ＢＥ：ＥＣ＝ＢＪ：ＩＣ＝９：２。

従って、
ＥＣ＝ＢＣ×２／１１＝５×２／１１＝１０／１１ｃｍ。

６．解答例５（沢井ねむ・るさん、他）

ＡＢ上にＢＦ＝６ｃｍとなる点Ｆを、
ＣからＡＦと平行に引いた直線と、ＦからＡＣに引いた直線の交点をＧ、そしてＡＥの延長とＣＧの交点をＨとします。参考図5

 ＡＦとＣＧは平行、ＡＣとＦＧは平行より、
四角形ＡＦＧＣは平行四辺形。
従って、ＣＧ＝ＡＦ＝１８ｃｍ、ＦＧ＝ＡＣ＝６ｃｍ。

∠ＡＦＧ＝∠ＡＣＨ、∠ＦＡＧ＝∠ＣＡＨ、
よって、△ＦＡＧ∽△ＣＡＨ。
従って、ＣＨ＝ＡＣ×ＦＧ／ＡＦ＝６×６／１８＝２ｃｍ。

ＡＢとＣＨが平行より、△ＡＢＥ∽△ＨＥＣ、
よって、ＢＥ：ＥＣ＝ＡＢ：ＨＣ＝９：２。

従って、
ＥＣ＝ＢＣ×２／１１＝５×２／１１＝１０／１１ｃｍ。

７．解答例６（みずなぎさん、他）

BからAD、 AEにそれぞれ垂線を引き、足を、Ｈ、I、
CからAE、ADにそれぞれ垂線を引き、足をJ、K
とします。参考図6

 ＢＨとＣＫは、ともにＡＨと垂直だから平行、
よって、△ＤＢＨ∽△ＤＣＫ、
従って、ＢＨ：ＣＫ＝ＤＢ：ＤＣ＝１：２＝３：６。・・（１）

∠ＢＡＨ＝∠ＣＡＪ、∠ＡＨＢ＝∠ＡＪＣ＝９０°、
よって、△ＡＢＨ∽△ＡＣＪ。
従って、ＢＨ：ＣＪ＝ＡＢ：ＡＣ＝９：６＝３：２。・・（２）

∠ＢＡＩ＝∠ＣＡＫ、∠ＡＩＢ＝∠ＡＫＣ＝９０°、
よって、△ＡＢＩ∽△ＡＣＫ。
従って、ＢＩ：ＣＫ＝ＡＢ：ＡＣ＝９：６。・・（３）

（１）、（２）、（３）より、ＢＩ：ＣＪ＝９：２。

ＢＩとＣＪは、ともにＡＩと垂直だから平行、
よって、△ＥＢＩ∽△ＥＣＪ、
よって、ＢＥ：ＥＣ＝ＢＩ：ＣＪ＝９：２。

従って、
ＥＣ＝ＢＣ×２／１１＝５×２／１１＝１０／１１ｃｍ。

８．解答例７（げんさん、他）

辺ＡＢ上にＡＦ＝４ｃｍとなる点Ｆをとり、
ＣＦとＡＥ との交点をＧとします。参考図7

 △ＡＢＣと△ＡＣＦについて、
∠ＢＡＣは共通で、ＡＢ：ＡＣ＝ＡＣ：ＡＦ＝３：２。
よって、△ＡＢＣ∽△ＡＣＦ。

∠ＣＡＧ＝∠ＢＡＤより、
ＣＧ：ＧＦ＝ＤＢ：ＤＣ＝１：２。

△ＦＢＣと直線ＡＥに関してメネラウスの定理より、
（ＦＡ／ＡＢ）・（ＢＥ／ＥＣ）・（ＣＧ／ＧＦ）＝１、
（４／９）・（ＢＥ／ＥＣ）・（１／２）＝１
よって、ＢＥ：ＥＣ＝９：２。

従って、
ＥＣ＝ＢＣ×２／１１＝５×２／１１＝１０／１１ｃｍ。

　９．解答例８（ET2世さん、他）

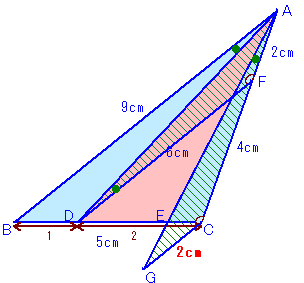
ＤからＡＢに平行な直線を引き、ＡＣとの交点をＦとします。参考図8

 ＡＢとＦＤは平行だから、△ＡＢＣ∽△ＦＤＣ。
よって、ＡＦ：ＦＣ＝ＢＤ：ＤＣ＝１：２。
ＡＦ＝ＡＣ×１／３＝２ｃｍ、ＦＣ＝４ｃｍ、
ＦＤ＝ＡＢ×２／３＝６ｃｍ。

次に、ＣよりＡＢに平行に直線を引き、ＣＧ＝２ｃｍとなるよう点Ｇをとります。

ＡＢとＣＧは平行より、∠ＡＦＤ＝∠ＧＣＡ。
ＡＦ＝ＧＣ＝２ｃｍ、ＤＦ＝ＡＣ＝６ｃｍ、
よって、△ＡＤＦ≡△ＧＡＣ。

このとき、∠ＧＡＣ＝∠ＡＤＦ＝∠ＢＡＤ＝∠ＥＡＣ、
よって、Ａ、Ｅ、Ｇは一直線上にあります。

ＡＢとＣＧは平行より、△ＡＢＥ∽△ＧＣＥ、
よって、ＢＥ：ＥＣ＝ＡＢ：ＧＣ＝９：２。

従って、
ＥＣ＝ＢＣ×２／１１＝５×２／１１＝１０／１１ｃｍ。

１０．解答例９（高橋道広さん、他）

AB上にAG＝６となる点Gをとり、
ACの延長線上にAF＝９となる点Fをとります。

図１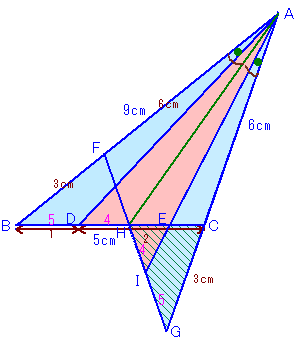
参考図9		 図２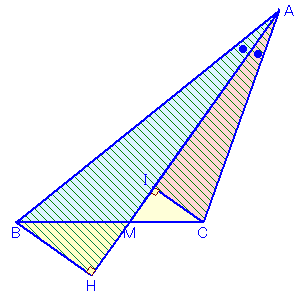
参考図9-1
BCとFGの交点をHとすると、AHは∠ＢＡＧの二等分線となります。 

すると、角の二等分線に関する定理より、BD：DH＝5：4となります。 
従って、AEとFGの交点をIとすると、ＧＩ：ＩＨ＝ＢＤ：ＤＨ＝５：４。

△ＨＧＣと直線ＡＩに関してメネラウスの定理より、
（ＨＥ／ＥＣ）・（ＣＡ／ＡＧ）・（ＧＩ／ＩＨ）＝１、
（ＨＥ／ＥＣ）・（６／９）・（５／４）＝１、
よって、ＨＥ：ＥＣ＝６：５。

従って、
ＥＣ＝ＨＣ×５／１１＝２×５／１１＝１０／１１ｃｍ。

１１．解答例１０（ヘロン久野さん、他）

ＡＢ上にＡＦ＝６ｃｍとなる点Ｆを、
ＡＣの延長線上にＡＧ＝９ｃｍとなる点Ｇをとります。
ＡＤの延長線とＢＧとの交点をＨ、ＦＣの交点をＩ、
ＡＥの延長線とＢＧとの交点をＪ、ＦＣとの交点をＫ
とします。参考図10

 △ＡＢＧはＡＢ＝ＡＧの二等辺三角形となり、ＦＣとＢＧは平行。
よって、ＡＦ：ＦＢ＝ＡＣ：ＡＧ＝６：３＝２：１。
従って、△ＡＦＩ∽△ＡＢＨ。
ＦＩ：ＢＨ＝２：３。・・・（１）

△ＢＡＨ≡△ＧＡＪより、ＦＩ＝ＫＣ、ＢＨ＝ＪＧ、
ＫＣ：ＪＧ＝２：３。・・・（２）

ＦＣとＢＧは平行より、△ＤＢＨ∽△ＤＣＩ。
よって、ＢＨ：ＣＩ＝ＢＤ：ＤＣ＝１：２＝３：６。
（１）、（２）より、
ＦＩ：ＩＫ：ＫＣ＝２：４：２、ＢＨ：ＨＪ：ＪＧ＝３：６：３。

また、△ＥＢＪ∽△ＥＣＫ、
よって、ＢＥ：ＥＣ＝ＢＪ：ＣＫ＝９：２。

従って、
ＥＣ＝ＢＣ×２／１１＝５×２／１１＝１０／１１ｃｍ。

１２．解答例１１（武田浩紀さん、他）

参考図11
（補題）ＡＢ2：ＡＣ2＝ＢＤ・ＢＥ：ＣＤ・ＣＥ。
これは、解答例６とほぼ同様にして証明できますが、次のように考えてみましょう。
（あまれっとさんの解法とほぼ同様）

ＡからＢＣに下ろした垂線の足をＨ、
∠ＢＡＤ＝∠ＣＡＥ＝α、∠ＢＡＥ＝∠ＣＡＤ＝βとすると、
△ＢＡＤ＝1/2・ＡＢ・ＡＤ・ｓｉｎα＝1/2・ＢＤ・ＡＨ
　　・・（１）
同様に、
△ＣＡＥ＝1/2・ＡＣ・ＡＥ・ｓｉｎα＝1/2・ＣＥ・ＡＨ 
　　・・（２）
△ＢＡＥ＝1/2・ＡＢ・ＡＥ・ｓｉｎβ＝1/2・ＢＥ・ＡＨ 
　　・・（３）
△ＣＡＤ＝1/2・ＡＣ・ＡＤ・ｓｉｎβ＝1/2・ＣＤ・ＡＨ
　 　・・（４）

（１）×（３）より、
ＡＢ2・ＡＤ・ＡＥ・ｓｉｎα・ｓｉｎβ＝ＢＤ・ＢＥ・ＡＨ2　・・（５）
（２）×（４）より、
ＡＣ2・ＡＤ・ＡＥ・ｓｉｎα・ｓｉｎβ＝ＣＤ・ＣＥ・ＡＨ2　・・（６）

（５）、（６）より、
ＡＢ2：ＡＣ2＝ＢＤ・ＢＥ：ＣＤ・ＣＥ。

補題より、
ＡＢ2：ＡＣ2＝ＢＤ・ＢＥ：ＣＤ・ＣＥ
９2：６2＝１・ＢＥ：２・ＣＥ．
よって、ＢＥ：ＣＥ＝９：４／２＝９：２。

従って、
ＥＣ＝ＢＣ×２／１１＝５×２／１１＝１０／１１ｃｍ。

（参考）他に、数学的な解法としては、

がありました。ちなみに、私自身はM.Hossieさんと全く同様に解きました。
数学的には、ごく素直な解法だと思います。