第242問の解答
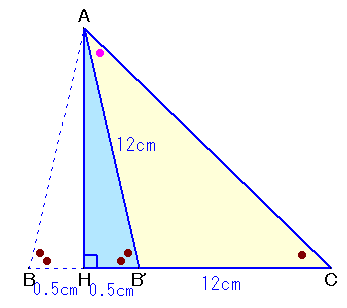
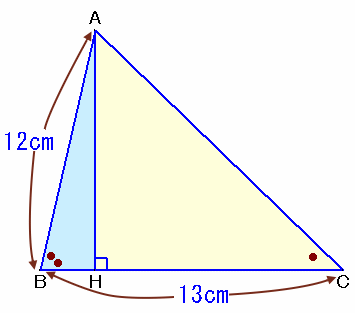
1.問題 [平面図形]
 |
|
2.解答例1(みみずくはくず耳さん、Taroさん、BossFさん、あやのりんさん、あんみつさん、圭太さん、木乃伊さん、他多数)
AHを軸に△ABHを折り返し、△AB'Hとする。
∠AB'H=∠B'AC+∠ACH
∠AB'H=∠ABH=2×∠ACH
従って、∠B'AC=∠ACH、すなわち△AB'Cは二等辺三角形となる。
よって、B'C=AB'=AB=12cm。BB'=BC−B'C=1cm。BH=B'H=1/2×BB=1/2×1=0.5、
HC=HB'+B'C=12.5cm。
よって、△ABH:△ACH=BH:HC=0.5:12.5=1:25。答:1:25
以上
3.解答例2(萬田銀次郎さん、C-Dさん、他)
AからBCに平行に引いた直線と∠Bの2等分線の交点をD、
DからBCに下ろした垂線の足をE、およびACとBDの交点をFとします。
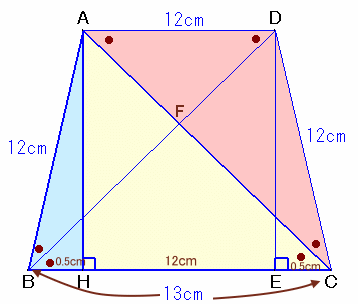
ADとBCが平行より、∠ADB=∠DBC=∠ABD、
よって△ABDは二等辺三角形、AD=AB=12cm。
HE=AD=12cm。ADとBCが平行より、∠DAC=∠ACB=∠ADB。
よって△AFDは二等辺三角形、AF=DF。また、∠FBC=∠FCBより、△FBCは二等辺三角形、FB=FC。
△ABDと△DCAについて、
AD=DA=12cm、BD=CA、∠ADB=∠DACとなり、
二辺挟角が等しいので合同。従って、AB=DC=12cm、∠ABD=∠DCA。
よって、△ABH≡△DCE。BH=EC=1/2×(BC−HE)=0.5cm、
HC=HE+EC=12.5cm、
よって、△ABH:△ACH=BH:HC=1:25。
4.解答例3(ちえんかん#2期さん、トトロ@Nさん、高橋道広さん、mhayashiさん、Hossさん、YokoyaMacさん、せいさん、他)
∠Bの二等分線とACの交点をD、およびDからBCに下ろした垂線の足をEとします。
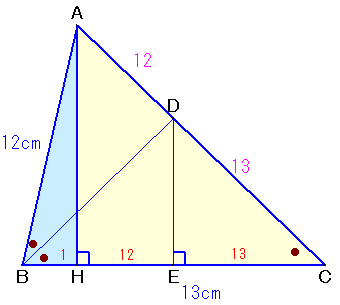
BDは∠ABCの二等分線だから、角の二等分線に関する定理より、AD:DC=AB:BC=12:13。
AHとDEが平行より、HE:EC=AD:DC=12:13。
∠DBC=∠DCBより、△DBCは二等辺三角形、BE=EC。
よって、BH:HC=(13−12):(13+12)=1:25。△ABH:△ACH=BH:HC=1:25。
(その他の解法)
- ・三角関数の倍角公式または半角公式等を用いる・・・・
きょえぴさん、noetherさん、中村明海さん、有無相生さん、M.Hossieさん、
DrKさん、中村亮さん、てつさん