第２５２問の解答

---

１．問題　［場合の数］

あるパーティに男性が５名、女性が５名参加しました。 この１０人はそれぞれ、参加者の異性の１人を好きになっており、しかもどの参加者も１人の異性に好かれているそうですが、残念ながら両想いは一組もないそうです。 では、このような関係は何通り考えられるでしょうか。

---

２．解答例１（ＴＯＲＡさん、高橋道広さん、ちえんかん＃２期さん、Michaelさん、ミミズクはくず耳さん、M.Hossieさん、小西孝一さん、他多数）

男性をM₁、M₂、・・、M₅、女性をF₁、F₂、・・、F₅とします。
M_mがF_nを好きだことを、M_m→F_nと表すことにします。

M₁→F₃→M₂→F₄→・・・、というように好きな異性を次々と並べていくと、M₁を好きな女性も１人いるので、最後はM₁に戻ってきます。

また、このとき男性、女性とも好きな異性が１人ずついることから、それぞれ同数いることになります。

そこで、男、女がn人ずついる場合をｎ組連鎖と呼ぶことにします。

１０人の男女では、５組連鎖と３組連鎖＋２組連鎖の２ケースが考えられます。（１組連鎖がありえないので、１組連鎖＋４組連鎖などはあり得ません）

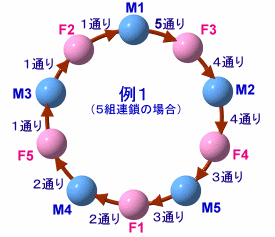
（１）５組連鎖の場合

M₁が選べる女性は、F₁〜F₅の５通り、（例１：F₃）
F₃が選べる男性は、M₁以外の４通り、（例１：M₂）
M₂が選べる女性は、F₃以外の４通り、（例１：F₄）
　　・・・
となり、合計
（５×４）×（４×３）×（３×２）×（２×１）×（１×１）＝２８８０通り
あります。

（２）３組連鎖＋２組連鎖の場合

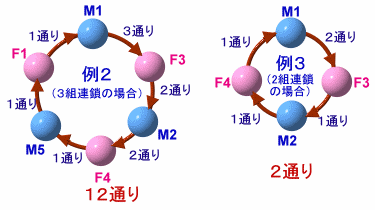
• ３組連鎖のとき
  ５組連鎖と同様にして、（３×２）×（２×１）×（１×１）＝１２通り
  
  
• ２組連鎖のとき
  同様にして、（２×１）×（１×１）＝２通り
  
  

となります。

このとき、３組連鎖に入る男女の組み合わせは、それぞれ₅C₃＝１０通りあり、残りの２組連鎖の組み合わせは自動的に決まります。

従って、３組連鎖＋２組連鎖の場合は、
　合計１０×１０×１２×２＝２４００通り
となります。

　

以上から、求める場合の数は、総計２８８０＋２４００＝５２８０通りとなります。

答：５２８０通り

以上

---

３．解答例２（医学部性さん、数楽者さん、noetherさん、トトロ＠Ｎさん、ヒデー王子さん、中村明海さん、長野美光さん、BossFさん、他）

まず男性がそれぞれ好きな女性を選ぶ選び方を考えます。

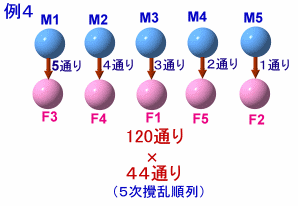
M₁が選べる女性は、F₁〜F₅の５通り、（例４：F₃）
M₂が選べる女性は、F₃以外の４通り、（例１：F₄）
　　・・・
となり、合計
　５×４×３×２×１＝１２０通り
あります。

次に、女性が好きな男性を選ぶ選び方は、それぞれ自分を好きな男性以外を選ぶことになるので、いわゆる５次の完全順列（攪乱順列ともいう）と考えられるので、４４通りとなります。

従って、合計１２０×４４＝５２８０通りとなります。

　

（参考）完全順列（攪乱順列）について（詳しくは類題：第２１２回問題を参照）

1、2、・・、n を一列に並べる順列のうち、 任意のk(1≦k≦n)に対して、 k番目がkでないような順列のことをn次の完全順列といいます。

• n次の完全順列の個数は、�納k=0..n](-1)^k・n!/k! で表すことができます。 
  ５次では、5!-5!/1!+5!/2!-5!/3!+5!/4!-5!/5!＝120-120+60-20+5-1＝44通り
  となります。
  
  
• 完全順列では，漸化式から求めることもできます。 
  ｎ次の完全順列の個数をｆ_nとすると、
  f₁=0、f₂=1、およびf_n＝ (n-1)(f_n-1＋f_n-2)が成り立つので、
  f₃＝2(1＋0)＝2、f₄＝3(2＋1)＝9、f₅＝4(9＋2)＝44
  と、順次求めることができます。
  
  
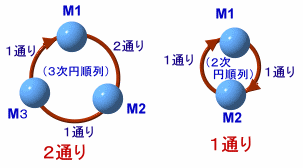
• あるいは、解答例１のn組連鎖の替わりにn次円順列を考えると、
  ５次の円順列＝5!/5＝２４通り
  ３次の円順列＋２次の円順列＝3!/3×2!/2×₅C₃＝２×１×１０＝２０通り
  合計２４＋２０＝４４通りと求めることもできます。

---