第２８６問の解答

問題　［平面図形］

問題図

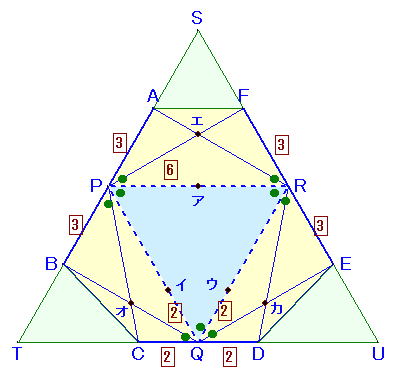
上の図は、あるフタのない立体Ｖの展開図です。

図中にある△ＰＱＲは正三角形で、各辺の長さの比は図にある通りになっています。
また、図中の●印（二重丸）の角度はすべて６０度です。

いま、辺ＰＲの中点をア、ＰＱを２：１に分ける点をイ、ＲＱを２：１に分ける点をウとします。
さらに、四角形ＡＰＲＦ、ＰＢＣＱ、ＲＱＤＥの対角線の交点をそれぞれエ、オ、カとします。

この立体を組み立てたとき（ＰＱ、ＱＲ、ＲＰが折り目です）、立体アイウ−エオカの体積は、立体Ｖの体積の何倍でしょうか。

解答例１
（トトロ＠Ｎさん、うっしーさん、C-Dさん、長野美光さん、ミミズクはくず耳さん、Taroさん、角田(＾＾)v鉄也さん、きょえぴさん、高橋道広さん、モルモット大臣さん、ふじさきたつみさん、M.Hossieさん、有無相生さん、さとけんさん、他多数）

［立体Ｖの体積］

まず、立体Ｖの体積を求めましょう。
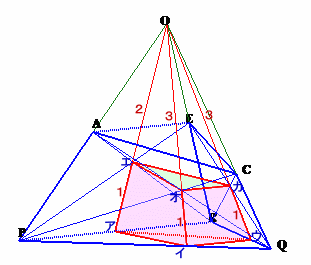
辺ＡＢ、ＣＤ、ＥＦをそれぞれ延長して交わる点をＳ、Ｔ、Ｕとします。

参考図１

●印の角度が全て６０度であることから、△ＳＰＲ、△ＰＴＱ、△ＲＱＵは全て△ＰＱＲと合同な正三角形となります。

従って、立体Ｖは△ＰＱＲを底面とする正四面体から頂点が同じ三角錐を除いたものとなります。

参考図２

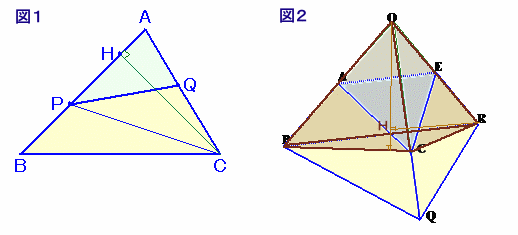
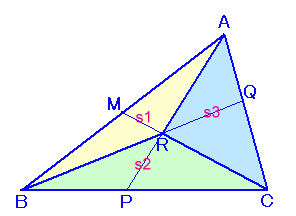
平面の場合を図１で考えると、△ＡＰＱ/△ＡＢＣ＝ＡＰ/ＡＢ×ＡＱ/ＡＣ。

参考図３

なぜなら、△ＡＰＣと△ＡＢＣは高さがＣＨで共通、底辺の長さはＡＰ：ＡＢ、
よって、△ＡＰＣ/△ＡＢＣ＝ＡＰ/ＡＢ。

同様に、△ＡＰＱ/△ＡＰＣ＝ＡＱ/ＡＣ。
従って、△ＡＰＱ/△ＡＢＣ
　＝（△ＡＰＣ/△ＡＢＣ）×（△ＡＰＱ/△ＡＰＣ）
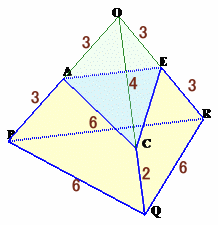
　＝ＡＰ/ＡＢ×ＡＱ/ＡＣ。

図２で、三角錐ＯＰＣＲ/三角錐ＯＰＱＲ＝ＯＣ/ＯＱ　・・・（１）
が成り立ちます。

なぜなら、三角錐ＯＰＣＲと三角錐ＯＰＱＲは高さがＲＨで共通、
底面の面積は△ＯＰＣ：△ＯＰＱ＝ＯＣ：ＯＱだからです。

同様に、
　三角錐ＯＡＣＲ/三角錐ＯＰＣＲ＝ＯＡ/ＯＰ、・・・（２）
　三角錐ＯＡＣＥ/三角錐ＯＡＣＲ＝ＯＥ/ＯＲ。・・・（３）

（１）×（２）×（３）より、
　三角錐ＯＡＣＥ/三角錐ＯＰＱＲ＝ＯＡ/ＯＰ×ＯＣ/ＯＱ×ＯＥ/ＯＲ　・・・（４）

よって、三角錐ＯＰＱＲの体積を１とすると、
　三角錐ＯＡＣＥの体積
＝ＯＡ/ＯＰ×ＯＣ/ＯＱ×ＯＥ/ＯＲ
＝３/６×４/６×３/６
＝１/２×２/３×１/２
＝１/６

従って、立体Ｖの体積＝１−１/６＝５/６。 ・・・（１）

［立体アイウ−エオカの体積］

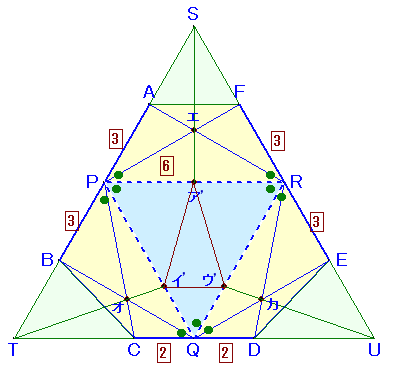
Sエの延長とＰＲの交点をア’、Ｔオの延長とＰＱの交点をイ’、Ｕカの延長とＱＲの交点をウ’とします。

参考図４

ア’、イ’、ウ’は実はア、イ、ウと一致します。

なぜなら、△ＳＰＲでチェバの定理より、
　（ＳＡ/ＡＰ）×（Ｐア’/ア’Ｒ）×（ＲＦ/ＦＳ）＝１
よって、
　３/３×（Ｐア’/ア’Ｒ）×３/３＝１
従って、Ｐア’/ア’Ｒ＝１となり、ア’はＰＲの中点、よってアと一致します。　

同様に、△ＴＱＰでチェバの定理より、
　（ＴＣ/ＣＱ）×（Ｑイ’/イ’Ｐ）×（ＰＢ/ＢＴ）＝１
よって、
　４/２×（Ｑイ’/イ’Ｐ）×３/３＝１
従って、Ｑイ’/イ’Ｐ＝２：４となり、Ｑイ’＝２ｃｍ、よってイと一致します。

△ＵＱＲは△ＴＱＰと合同なので、ウ’もウと一致することが分かります。


参考図５

また、チェバの定理の補題により、
　Sエ/エア＝SA/AP+SF/FR=３/３+３/３=２/１
　Tオ/オイ＝TB/BP+TC/CQ=３/３+４/２=３/１
　Uカ/カウ＝UD/DQ+UE/ER=４/２+３/３=３/１

さて、△アイウの底辺の長さは、イウ＝PR×１/３
また、高さ＝△PQRの高さ×２/３
よって、△アイウの面積
　＝△PQRの面積×１/３×２/３
　＝△PQRの面積×２/９

従って、三角錐O−アイウの高さは、正四面体O−PQRの高さと共通だから、体積は底面の面積比＝２/９。

あとは、立体Vの体積と同様にして、
　立体アイウ−エオカの体積
＝（三角錐O−アイウ）×（１-２/３×３/４×３/４)
＝２/９×５/８
＝５/３６ ・・・（２）

従って、
　立体アイウ−エオカの体積／立体Vの体積
＝（５/３６）／（５/６）
＝１/６倍
となります。

［参考１］動く３Ｄ図

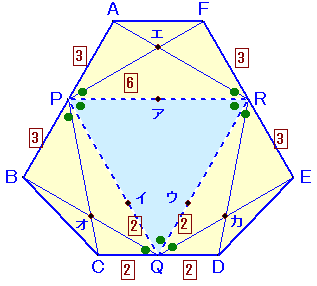
［参考２］チェバの定理

（チェバの定理）
Rを三角形の内部の点とし、ARの延長と辺BCの交点をP、ARの延長と辺BCの交点をP、BQの延長と辺CAの交点をQ、CRの延長と辺ABの交点をMとす ると、次式が成り立つ。

　参考図１
(AM/MB)・(BP/PC)・(CQ/QA)＝１

（証明）
s1＝△ABR、s2＝△BCR、s3＝△CARとします。
△ABP：△APC＝△RBP：△RPC＝BP：PC。
よって、s1：s3＝(△ABP−△RBP)：(△APC−△RPC)＝BP：PC。
　　・・・　（１）

同様に、
　s2：s1＝CQ：QA ・・・　（２）、　s3：s2＝AM：MB ・・・　（３）

（３）×（１）×（２）より、
　(AM/MB)・(BP/PC)・(CQ/QA)＝(s3/s2)・(s3/s2)・(s3/s2)＝１

 （補題）
左図で、次式が成り立つ。
　AR/RP＝QA/CQ＋AM/MB、
　BR/RQ＝MB/AM＋BP/PC、
　CR/RM＝PC/BP＋CQ/QA

（証明）
　AR/RP＝△ABR/△RBP＝s1/(s2×BP/BC)、
　AR/RP＝△ARC/△RPC＝s3/(s2×PC/BC)。

よって、
　(AR/RP)×(BP/BC)＋(AR/RP)×(PC/BC)
　　＝s1/s2＋s3/s2
従って、
　AR/RP
＝s1/s2＋s3/s2
＝QA/CQ＋AM/MB

他も同様。　

　


　

答：１/６倍

以上

（その他の解法）

・正四面体・三角錐から小さい三角錐を切り取る　・・・　あんみつさん他

・ルートを使って両方の体積を計算　・・・　まおさん他