第２９６問の解答

---

問題　［平面図形］

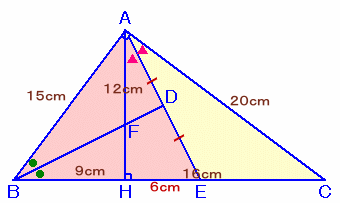
上の図のような∠Ａ＝９０゜の直角三角形ＡＢＣがあり、頂点Ａから辺ＢＣに降ろした垂線の足をＨとします。 また、△ＡＢＨの周の長さが３６cm、△ＡＨＣの周の長さが４８cmとなっています。 いま、∠Ｂの二等分線と∠ＨＡＣの二等分線の交点をＤとします。 このとき、△ＡＢＤの面積を求めてください。

---

解答例１（Taroさん、CRYING DOLPHINさん、ミミズクはくず耳さん、あんみつさん、あまれっとさん、拓パパさん、おかひで博士さん、sodoさん、岩間美顕さん、ふじさきたつみさん、モルモット大臣さん、有無相生さん、数楽者さん、N.Nishiさん、他多数）

ADの延長線と辺BCの交点をEとし、AHとBDの交点をFとします。

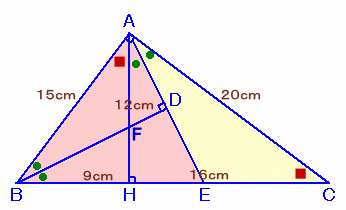
△ABHは直角三角形だから、∠BAH＝９０度−∠ABH。
△CBAも直角三角形だから、∠BCA＝９０度−∠ABH。
よって、∠BAH＝∠BCA。

従って、△ABH、△CAH、△CBAは相似。

題意より、△ABHと△CAHの相似比は、
　△ABHの周囲の長さ：△CAHの周の長さ＝３６：４８＝３：４。

従って、BH：AH＝３：４となり、△ABH、△CAH、△CBAは全て辺の長さが３：４：５の直角三角形となります。 　・・・　（１）

よって、∠CAH＝∠ABHとなるので、△AFDと△BFHは２角が等しいので相似、
従って、∠ADF＝∠BHF＝９０度。　・・・　（２）

よって、△ABDと△EBDはBDが共通で、これを挟む２角が等しいので合同、
従って、△ABEはAB＝BE＝１５cmの二等辺三角形となります。

△ABD＝△ABE×1/2＝1/2×BE×AH×1/2＝1/2×１５cm×１２cm×1/2＝４５cm²

答：４５cm²

以上

---

解答例２（ねこやんさん、前田先生＠P進学院さん、小西孝一さん、角田(^^)v鉄也さん、 他）

（１）までは、解答例１と同じ。

△AHCにおいて、角の二等分線の定理より、HE：EC＝AH：AC＝３：５。
よって、HE＝HC×３/８＝１６×３/８＝６cm。
従って、BE＝BH＋HE＝９＋６＝１５cm。

△ABEにおいて、角の二等分線の定理より、AD：DE＝AB：BE＝１：１。
よって、△ABD＝△ABE×1/2＝1/2×BE×AH×1/2＝1/2×１５cm×１２cm×1/2＝４５cm²

---

解答例３（ハラギャーテイさん、M.Hossieさん、Parpunteさん、信三さん、QPerさん、やまはらさん、takuさん、他）

（２）まで、解答例１と同じ。

∠ABD＝∠EBD＝θとおくと、sin2θ＝4/5、cos2θ＝3/5。

△ABD＝1/2×BD×AD＝1/2×（AB×cosθ）×（AB×sinθ）
＝1/2×AB²×cosθsinθ＝1/4×１５²×２cosθsinθ＝1/4×１５²×sin2θ
＝1/4×１５²×4/5＝４５cm²

---