第３１３問の解答

---

問題　［平面図形］

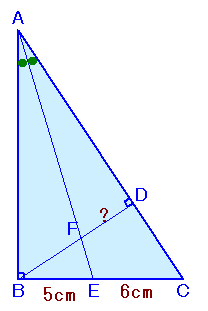		左図のような、∠Ｂ＝９０度の直角三角形ＡＢＣがあります。 いま、∠Ａの二等分線をひいたところ、辺ＢＣと点Ｅで交わり、ＢＥ＝５cm、ＣＥ＝６cmとなりました。 では、頂点Ｂから辺ＡＣに下ろした垂線の足をＤとし、ＡＥとの交点をＦとするとき、ＦＤの長さを求めて下さい。

---

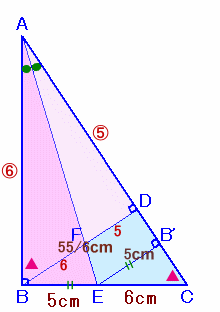
解答例１

うっしーさん、まるケンさん、永井　暁さん、CRYING DOLPHINさん、拓パパさん、emikoさん、ちば けいすけさん、ねこやんさん 、 かめちゃんさん、他

	辺ＡＥを軸にして△ＡＢＥを折り返したものを△ＡＢ'Ｅとします。 すると、Ｂ'Ｅ＝ＢＥ＝５ｃｍ。 また、ＢＤとＥＢ'は平行だから、△ＣＢＤと△ＣＥＢ'は相似、 よって、ＢＤ：ＥＢ'＝ＢＣ：ＥＣ＝１１：６。 △ＢＤＡも△ＣＢ'Ｅと相似なので、ＡＢ：ＡＤ＝ＣＥ：ＥＢ'＝６：５。 また、△ＡＢＥと△ＡＤＦは相似な直角三角形だから、 　ＢＥ：ＤＦ＝ＡＢ：ＡＤ＝６：５。 よって、ＦＤ＝ＢＥ×５/６＝５×５/６＝２５/６ｃｍ。 なお、△ＡＣＥをＡＥを軸として折り返しても、同様な解法になります。 （かめちゃんさん、他） 　 答：　２５/６ｃｍ 以上

---

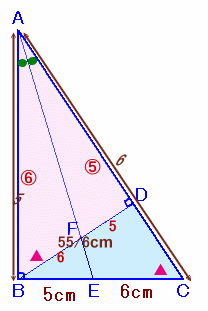
解答例２

長野　美光さん、Banyanyanさん、ＩＣさん、高田修成さん、クララさん、トトロ＠Ｎさん、小西孝一さん、M.Hossieさん、kokoさん、ふじさきたつみさん、他

	三角形の角の二等分線に関する公式を用います。 △ＡＢＣで、ＡＥは∠ＢＡＣを二等分するから、ＡＢ：ＡＣ＝ＢＥ：ＥＣ＝５：６。 △ＢＤＣと△ＡＢＣは相似より、ＢＤ：ＢＣ＝ＡＢ：ＡＣ＝５：６、 よって、ＢＤ＝ＢＣ×５/６＝５５/６ｃｍ。 また、△ＡＤＢも△ＡＢＣと相似より、ＡＤ：ＡＢ＝ＡＢ：ＡＣ＝５：６。 さらに、△ＡＢＤで、ＡＦは∠ＢＡＤを二等分するから、ＢＦ：ＦＤ＝ＡＢ：ＡＤ＝６：５、 よって、ＦＤ＝ＢＤ×５/１１＝５５/６×５/１１＝２５/６ｃｍ。

---

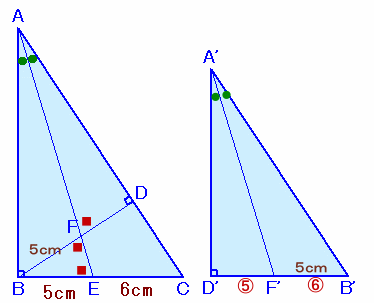
解答例３

あんみつさん、ガンマ先生さん、他

	△ＡＢＤをＡＤを軸として折り返したものを、△Ａ'Ｂ'Ｄ'とします。 まず、∠ＢＦＥ＝∠ＡＦＤ＝９０°−∠ＦＡＤ＝９０°−∠ＢＡＥ＝∠ＢＥＦ。 従って、△ＢＥＦは、ＢＥ＝ＢＦ＝５ｃｍとなる二等辺三角形となります。 さて、△ＡＢＣと△Ａ'Ｄ'Ｂ'、△ＡＢＥと△Ａ'Ｆ'Ｂ'、△ＡＥＣと△Ａ'Ｆ'Ｂ'は、それぞれ相似だから、 　Ｄ'Ｆ'：Ｆ'Ｂ'＝ＢＥ：ＥＣ＝５：６。 従って、ＦＤ＝ＦＢ×５/６＝５×５/６＝２５/６ｃｍ。

---

（その他の解法）

• ピタゴラスの定理等をもちいる　・・・　Taroさん、 他
• 三角関数を用いる　・・・　ハラギャーテイさん、他
• 座標をもちいて計算する　・・・　有無相生さん、他