第３２１問の解答

問題　［空間図形］

問題図

左図は、底面が面積１２８cm2の正方形であるような角柱を３本、それぞれが垂直に交わるように組み合わせたものです。

この場合、３本の角柱の共通部分は立方体になりますね。

では、この３本の角柱をそれぞれ４５度回転させたとき、３本の角柱の共通部分の体積は何cm3でしょうか。

はじめに

類題が「算チャレVer.２」第８３問にあります。こちらも参考にして下さい。

さて、３本の角柱の共通部分が、どんな立体になるのかを調べてみましょう。

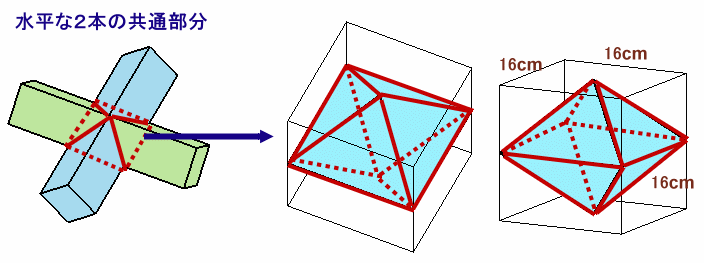
最初に、水平な２本の共通部分を考えます。
下図のように、角柱底面の対角線の長さ１６cmを１辺とする立方体にすっぽり入る八面体になります。
この八面体は、１辺が１６cmの正方形を底面とする正四角錐を２個合わせた形になっています。

参考図０−１

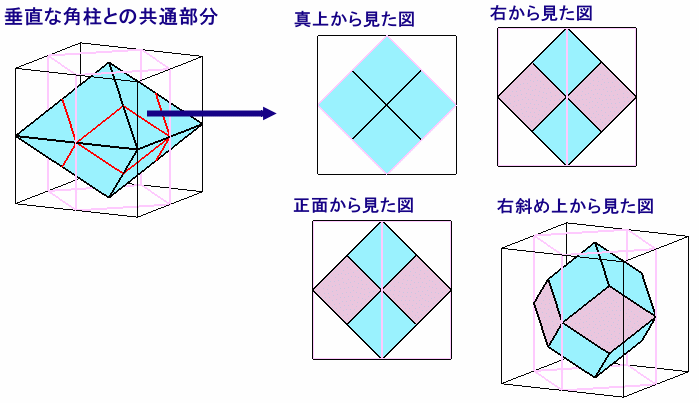
さらに、この八面体と垂直な角柱との共通部分が、どうなるかを考えてみましょう。

これは、立方体の４隅を垂直に切断することと同じですから、八面体の４隅を切断した１２面体となることが分かります。なお、この１２面体は、同じ大きさの菱形１２枚からできています。

参考図０−２

　

（参考）マウスでドラッグして下さい。

　

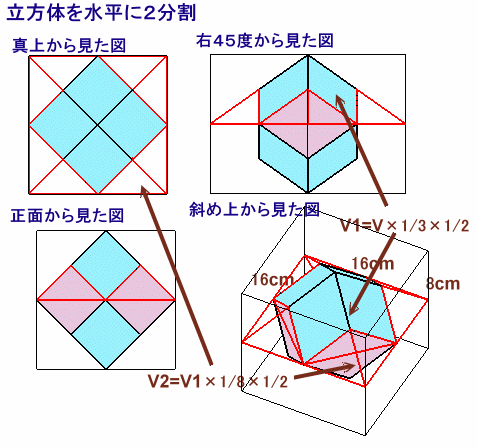
解答例１

sodoさん、ＴＯＲＡさん、VILLさん、トトロ＠Ｎさん、ミミズクはくず耳さん、おおおさん、たけのしんさん、フランク長いさん、ねこやんさん、他

立方体の体積をＶとし、立方体を水平に切断して上半分で考えます。

参考図１

正四角錐の体積をＶ１、４隅の三角錐の体積をＶ２、１２面体の体積をＶ３とします。

Ｖ１＝Ｖ×１/３×１/３（底面は立方体と同じ、高さは立方体の半分）
　　＝Ｖ×１/６

Ｖ２＝V1×１/１６（底面積：１/８、高さ：１/２）

Ｖ３＝（Ｖ１−Ｖ２×４）×２
　　＝（Ｖ１−Ｖ１×１/１６×４）×２
　　＝Ｖ１×３/４×２
　　＝（Ｖ×１/６）×３/２
　　＝Ｖ×１/４
　　＝１６×１６×１６×1/４
　　＝１０２４cm3

答：　１０２４cm3

以上

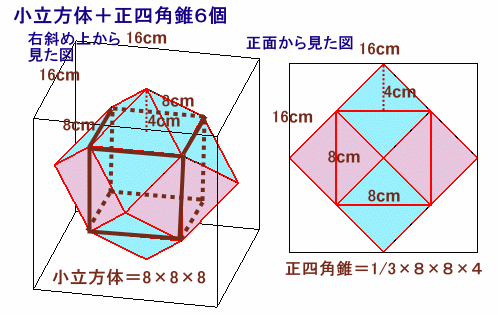
解答例２

まるケンさん、中村明海さん、ふじさきたつみさん、 他

１２面体を小立方体とその各面に正四角錐を貼り付けたものとして考えます。

参考図２

小立方体の１辺＝元の立方体の１辺×１/２＝８cm。
小立方体の体積＝８×８×８＝５１２cm3。

正四角錐の底面：１辺8cm、高さ＝１６×１/４＝４cm。
正四角錐の体積＝１/３×８×８×４＝２５６/３cm3。

よって、１２面体の体積
　＝小立方体＋正四角錐×６
　＝５１２＋２５６/３×６
　＝５１２＋５１２
　＝１０２４cm3。

なお、正四角錐を小立方体の内側にそれぞれおくと、６個で小立方体を埋め尽くすので、
　正四角錐×６＝小立方体となります。

解答例３

CRYING DOLPHINさん、高橋　道広さん、他

立方体を８等分した小立方体で考えます。
切断図は下図のようになります。

参考図３

小立方体の１辺＝元の立方体の半分＝８cm。

１２面体の切断は、２つの三角錐V１、V2に分割できます。

V１＝１/３×８×（１/２×８×８）＝２５６/３cm3。

V２＝V１×１/２。

よって、１２面体の体積
＝（V1＋V２）×８
＝V1×３/２×８
＝２５６/３×１２
＝１０２４cm3。

（その他の解法）