第375問の解答
問題[空間図形]
|
|
|
|
|
|
|
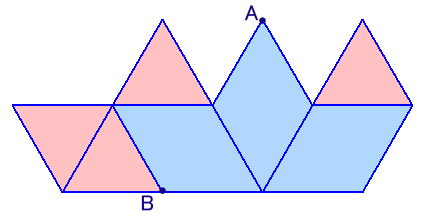 |
左図は、正三角形と菱形を組み合わせた、ある立体の展開図を表しています。 この展開図を組み立てて立体を作ったとき、展開図中の点Aと点Bの距離は6cmになります。 この立体の体積を求めてください。 |
|
|
|
|
|
|
解答例1
角さん、CRYING DOLPHINさん、まるケンさん、はなうさん、長野 美光さん、トトロ@Nさん、拓パパさん、中村明海さん、ミミズクはくず耳さん、M.Hossieさん、namaさん、 他多数
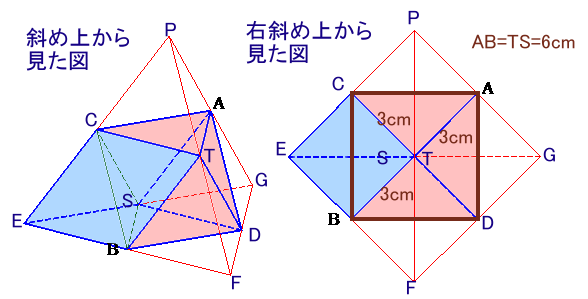
菱形の角が小さい頂点3つが集まる部分に注目すると、下図のように立体は正四面体と正八面体が合体したものと分かります。
また、辺の長さが2倍の正四面体を考えると、求める立体は大きい正四面体から小さい正四面体を3個取り除いたものとなっています。
大きい正四面体の体積は、小さな正四面体の体積(Vとします)の23=8倍なので、
正八面体の体積=V×4、求める立体の体積=V×5、
従って、
求める立体の体積=正八面体の体積×5/4
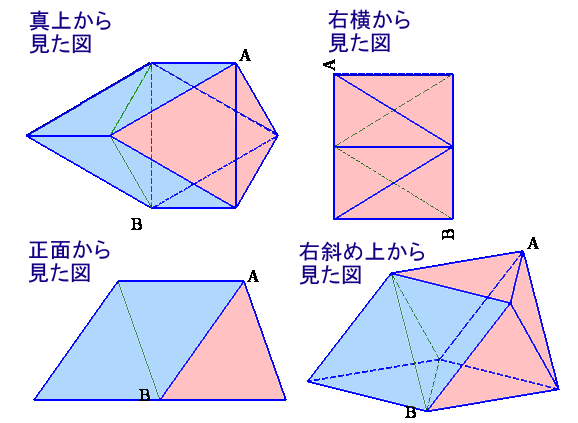
となります。(参考:第131問)さて、正八面体を平面ACBDで2つの四角錐に分割して体積を求めてみましょう。
ABは底面である正方形ACBDの対角線となっているので、
ABCDの面積=32×2=18cm22つの四角錐の高さも3cmなので、
正八面体の体積=1/3×18×3×2=36cm3
となります。従って、求める立体の体積=36×5/4=45cm3
と求まります。答: 45cm3
以上
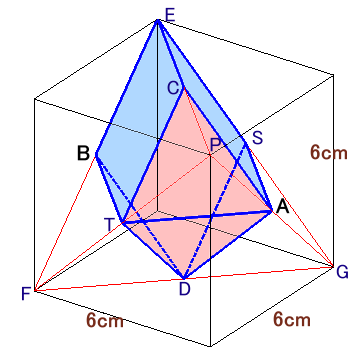
(別解)大きな正四面体を内接する立方体から求めてみます。
A、Bは立方体の相対する面の中心となっているので、
立方体の1辺の長さ=AB=6cm
となります。大きな正四面体は、立方体から三角錐4個を除いた形となっているので、
大きな四面体の体積=63−1/3×(1/2×62)×6×4=72cm3
となります。従って、
求める立体の体積=72cm3×5/8=45cm3
と求まります。
(参考)マウスでドラッグして下さい。
(その他の解法)
- 印刷し紙工作で解いた、ポリドロンで組み立てた ・・・ kasamaさん、Taroさん、クララさん、トトロ@Nさん、みかんさん、UnderBirdさん、ハラギャーテイさん、すてっぷさん、ちずさん、ユイさん、大岡 敏幸さん、他 多数
- 1辺の長さを求めて解く ・・・ みかんさん、小西孝一さん、ねこやんさん、大岡 敏幸さん、 他