第390問の解答
問題[場合の数]
|
|
|
|
|
|
|
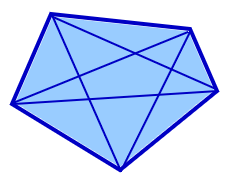 |
左図のように、凸型の5角形の対角線を全て引くと、5角形の内部は11個の小多角形に分割されます。 では、凸型10角形の対角線を引けるだけ引くと、10角形の内部は何個の小多角形に分割されるでしょうか。 |
|
|
|
|
|
|
解答例1
あ〜く@旧Nさん、AЯOTさん、CRYING DOLPHINさん、長野美光さん、小学名探偵さん、萬田銀次郎@昼休みさん、他
一般的な凸n角形の場合で考えることにとします。
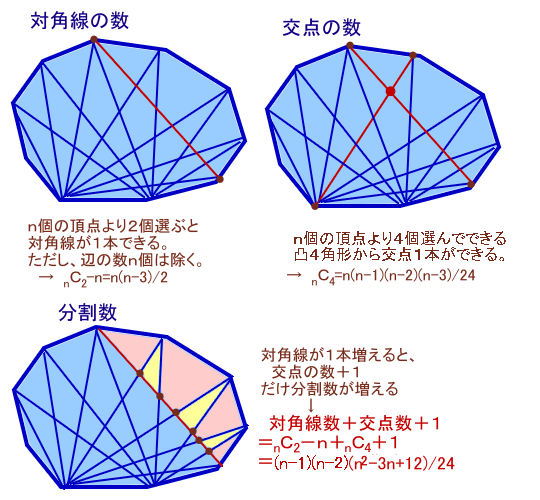
まず、凸n角形の対角線、および交点の個数を数えてみましょう。
各対角線は、n個の頂点から2個を選んで、線分を引くことによって決まるので、
nC2本となりますが、このうち凸n角形の辺と一致するn本は除く必要があるので、
対角線数=nC2−n=n(n−1)/2−n=n(n−3)/2本 ・・・ (1)
と求まります。また、各交点はn個の頂点から4個の頂点を選らんでできる凸4角形の対角線の交点として決まるので、
交点数=nC4=n(n−1)(n−2)(n−3)/24個 ・・・ (1)
と求まります。さて、凸n角形で対角線を引く前には、分割数は1であり、
対角線を1本引くたびに、交点の数+1だけ分割数が増えることから、
凸n角形の分割数
=対角線数+交点数+1
=n(n−3)/2+n(n−1)(n−2)(n−3)/24+1
=(n−1)(n−2)(n2−3n+12)/24
と求まります。とくに本問では、n=10として、
凸n角形の分割数
=(10−1)(10−2)(102−3×10+12)/24
=246個
と求まります。答: 246個
以上
(参考)算チャレVer2 第74問
こちらは円周上にとったn点を結んだときの分割数なので、本問よりn個多い結果となります。
解答例2
ミキティさん、なかさん、トトロ@Nさん、ゴンともさん、小西孝一さん、ハラギャーテイさん、他
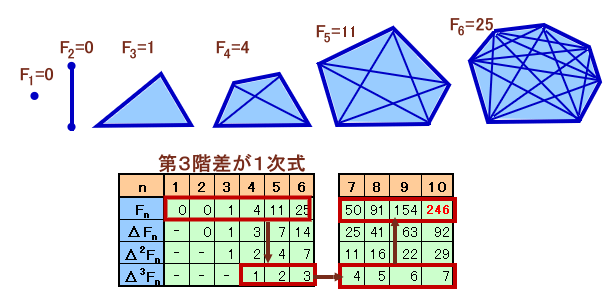
凸n角形の分割数をFnとします。
n=1から6までの凸n角形を描いて数えると、
分割数=0、0、1、4、11、25
となります。これらから、階差数列を3次まで求めると、
1、2、3
と1次式になると予想されます。この予想をもとに、n=7から10まで計算すると、
分割数=50、91、154、246
となります。
(参考)数列大辞典にも掲載
(その他の解法)
- 漸化式をたてて解く ・・・ 拓パパさん、とまぴょんさん、 他
凸(n−1)角形に、新たに一点を加え凸n角形をつくる。
その加えた点から新たな対角線が(n−3)本引けるので、
そのときに増加する分割数は
Σ(k=1.. n-3) {k(n-2-k)} + (n-3) +1
となる。
これから漸化式をたて、一般式(n-1)(n-2)(n2-3n+12)/24を得る。
- 実際に図を描き数え上げる ・・・ いちたすにはさん、きょろ文さん、スモークマンさん、M.Hossieさん、kasamaさん、他