第414問の解答
問題[平面図形]
|
|
|
|
|
|
|
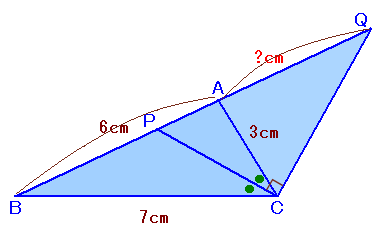 |
左図で、△ABCはAB=6cm、BC=7cm、CA=3cmとなっています。 いま、∠Cの二等分線と辺ABの交点をPとし、直線AB上に、∠PCQ=90°となるような点Qをとりました。 このとき、AQの長さを求めてください。 |
|
|
|
|
|
|
解答例1
CRYING DOLPHINさん、AMさん、姉小路さん、DIDDYKONGさん、他
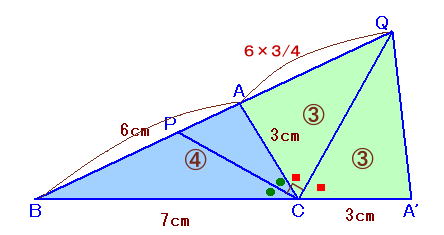
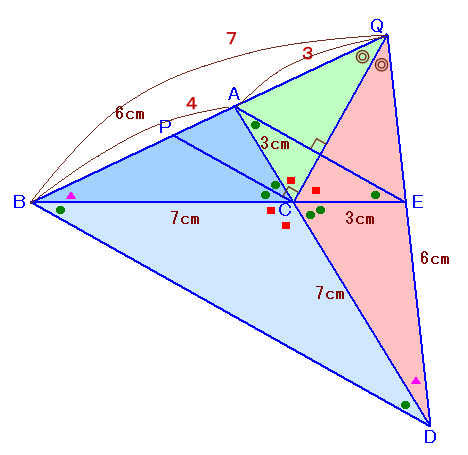
辺QCを軸にして、△QACを折り返したものを△QA’Cとします。
∠QCB+∠QCA’
=(∠PCB+∠ACP+∠QAC)+∠QCA’
=∠ACP×2+∠QCA×2 (∠PCB=∠ACP、∠QAC=∠QCA'より)
=(∠ACP+∠QCA)×2
=90°×2=180°よって、B、C、A’は一直線上に並びます。
すると、
△QBCの面積:△QCA’の面積=BC:CA’=7:3
よって、
△QBC=10とすると、△QBC=7、△QCA’=3
△ABC=△QBC−△QAC=△QBC−△QCA’=7−3=4従って、
AB:QA=△ABC:△QCA’=4:3よって、
AQ=AB×3/4=6×3/4=9/2=4.5cm
と求まります。答: 4.5cm
以上
解答例2
マサルさん 、Plutonianさん、数楽者さん、他
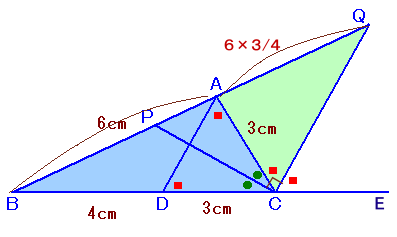
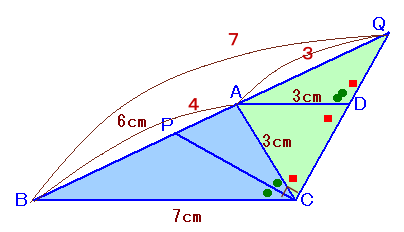
点Aを通り辺QCに平行に引いた直線とBCの交点をDとし、BCの延長線上に適当な点Eをとります。
∠QCE
=180°−(∠PCB+∠ACP+∠ACQ)
=180°−(∠PCB+90°)
=90°−∠PCB=∠ACQADとQCは平行だから、
∠CAD=∠ACQ(錯角)、∠CDA=∠ECQ(同位角)より、∠CAD=∠CDAよって、△CADは二等辺三角形となります。
従って、CD=CA=3cm、BD=7−3=4cm。ADとQCは平行だから、
AB:AQ=BD:DC=4:3 ・・・ (1)よって、
AQ=AB×3/4=6×3/4=9/2=4.5cm
と求まります。なお、この解法は、角の二等分線の定理(外角)の証明と同様です。
この定理を用いると、 QB:QA=CB:CA=7:3から(1)がすぐに分かります。
解答例3
DrKさん他
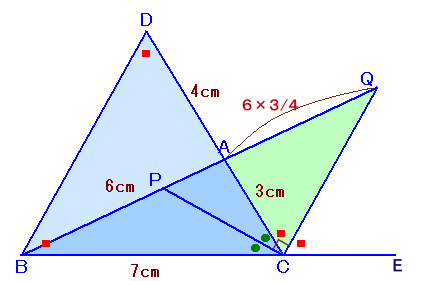
点Bを通り辺CQと平行に引いた直線と、CAの延長線の交点をDとします。
解答例2と同様にして、∠QCE=∠ACQとなります。
DBとQCは平行だから、
∠CDB=∠QCD(錯角)、∠CBD=∠ECQ(同位角)より、∠CDB=∠CBDよって、△CDBは二等辺三角形となり、CD=BC=7cm、AD=7−3=4cm。
さて、DBとQCは平行だから、△ADBと△ACQは相似。
よって、
AB:AD=AQ:AC、
AQ=AB×AC/AD=6×3/4=9/2=4.5cm
と求まります。
解答例4
小西孝一さん、きょろ文さん、他
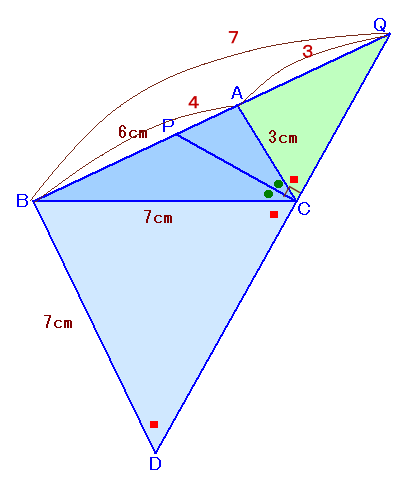
点Bを通り辺ACと平行に引いた直線とQCの延長線の交点をDとします。
∠BCD=180°−(∠PCB+∠ACP+∠ACQ)=90°−∠PCB=∠ACQ、
および∠BDC=∠ACQ(同位角)より、∠BCD=∠BDC。よって、△BDCは二等辺三角形となり、BD=BC=7cm。
ACとBDは平行だから、
QA:QB=AC:BD=3:7よって、AQ=AB×AC/AD=6×3/4=9/2=4.5cm
と求まります。
解答例5
takuさん他
点Bを通り辺PCと平行に引いた直線とACの延長線の交点をDとし、BCの延長線とQDの交点をEとします。
PCとBDは平行だから、
∠CBD=∠PCB(錯角)、∠CDB=∠PCB(同位角)より、∠CBD=∠CDB、
よって、△CBDは二等辺三角形となり、CD=CB=7cm。∠QCE=∠ACQ(解答例2と同様)、∠ECD=∠ACB(対頂角)より、
∠ACD=∠QCE+∠ECD=∠ACQ+∠ACB=∠QCB。すると、△QCBと△QCDについて、二辺挟角が等しいので合同、
よって、∠BQC=∠DQC、∠QBC=∠QDCとなります。今度は、△QCAと△QCEについて、1辺と両端の角が等しいので合同、
よって、CE=CA=3cm。従って、△CAEはCA=CEの二等辺三角形となり、∠CAE=∠CEA。
よって、△CAEと△CBDは、∠ACE=∠BCDより、頂角が等しい二等辺三角形なので相似。
従って、AEとBDは平行、AE:BD=CA:BD=3:7となります。よって、
AQ:QB=AE:BD=3:7
AQ=AB×3/4=6×3/4=9/2=4.5cm
と求まります。
解答例6
uchinyanさん他
点Aを通り辺BCと平行に引いた直線と辺QCの交点をDとします。
∠QDA=∠QCB(同位角)より、
∠ADC=180°−∠QDA=180°−∠QCB=180°−(∠PCB+∠ACP+∠ACD)
=180°−∠PCB=∠ACDよって、△ACDは二等辺三角形となり、AD=AC=3cm。
ADとBCは平行だから、
QA:QB=AD:BC=3:7よって、
AQ=AB×3/4=6×3/4=9/2=4.5cm
と求まります。
(その他の解法)
AQ上にPA=QRとなる点Rをとる。点CからAQ上に垂線CHを引く ・・・ トトロ@N さん、他
△RBCと△ACHはともに直角を挟む2辺の比が3:7の直角三角形になること からAP:PB=3:7となることを利用角の二等分線の定理」と「平行線」を使う ・・・ 始 受験勉強君 さん、他
最終的には、3×1.8/1.2=9/2cm垂線引いて、二等辺三角形を作る ・・・ ari-june さん、他
引いた垂線が、三角形の一辺と平行なので6かける3/4三角関数を使って解く ・・・ tomhさん、ゴンともさん、ハラギャーテイさん、uchinyanさん、他
CAD等で作図して解いた ・・・ kasamaさん、M.Hossieさん、他