第423問の解答
問題[空間図形]
|
|
|
|
|
|
|
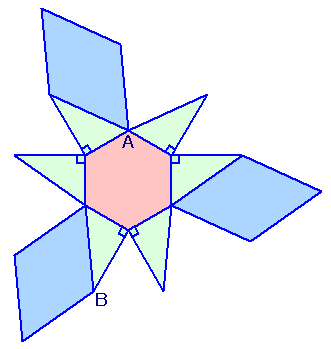 |
左図のような、1枚の正六角形と、3枚の菱形、6枚の直角三角形でできた立体の展開図があります。 正六角形と菱形の面積は等しく、組み立てた立体において、図中のAとBを結んだ線分の長さは6cmとなるということです。 このとき、この立体の体積を求めてください。 |
|
|
|
|
|
|
解答例1
おかひで博士さん、はなうさん、tomhさん、アヒーのおじさんさん、uchinyanさん、ほげさん、ゴンともさん、n厨さん、M.Hossieさん、DrKさん、トトロ@Nさん、ドイルさん、水田Xさん、N.Nishiさん、姉小路さん、他
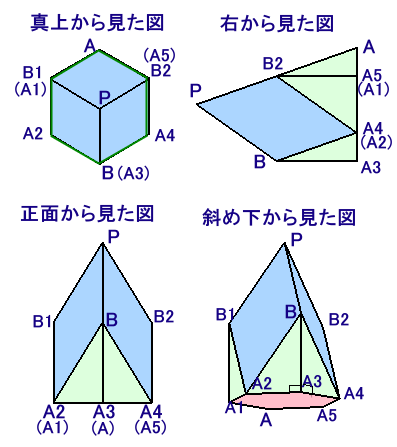
展開図をもとに立体を組み立てると下図のようになります。
上側の頂点をP、底面の正六角形の頂点を時計回りにA、A1、A2、A3、A4、A5、および中間に来る菱形の頂点をB1、B、B2とします。
A1、A3、A5で、それぞれ2つの直角三角形が隣り合っているので、これらは底面と垂直になっています。
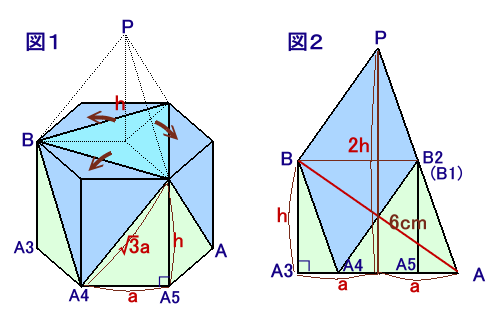
また、対称性などからB1、B、B2は、Pと底面のちょうど中間の高さにあり、この3点を結ぶと正三角形になります。B1BB2で立体を切断し、上側の正四面体を3分割します。これら下側の斜めの面に合わせると、ちょうど正六角柱ができることが分かります。
この正六角柱の高さは(hとします)、もとの立体の高さの半分になります。
さて、底面の正六角形で1辺の長さをa、菱形の1辺の長さをbとします。
正六角形は、1辺の長さがaの正三角形が6個、菱形は1辺の長さがbの正三角形が2個からなっていますので、題意より、
1/4×√3×a2×6=1/4×√3×b2×2従って、
b=√3×a ・・・ (1)
が成り立ちます。すると、図1、図2の直角三角形の3辺の長さより、
a2+h2=(√3×a)2 ・・・ (2)
(2×a)2+h2=62 ・・・ (3)
が成り立ちます。(1)、(2)、(3)より、
a=√3、b=3√2、h=2√3
を得ます。従って、
求める立体の体積
=正六角柱の体積
=(1/4×√3×a2)×6×h
=54cm3
と求まります。答: 54cm3
以上
解答例2
あ〜く@ぴかぴかの(略さん、貞松 篤さん、mhayashiさん、すてっぷさん、takaisaさん、小学名探偵さん、 他
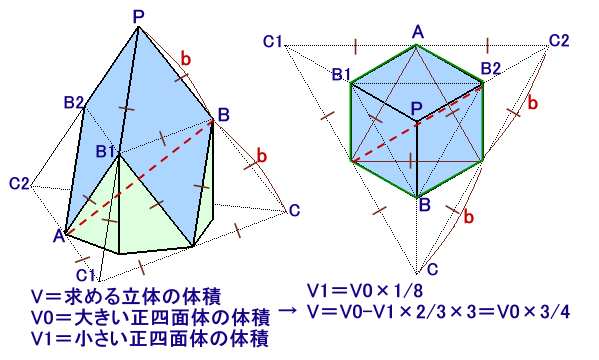
PB1、PB、PB2を延長して底面と交わる点をC1、C、C2とします。
すると、三角錐PC1CC2は、1辺の長さが2bの大正四面体となります。
大正四面体の体積=√2/12×(2b)3=72cm3となります。(第131問解答例3)また、求める立体は、この大正四面体から1辺の長さがbの小正四面体の2/3を3個取り除いたものとなっているので、
求める立体の体積
=72×(1−1/8×2/3×3)
=72×3/4
=54cm3
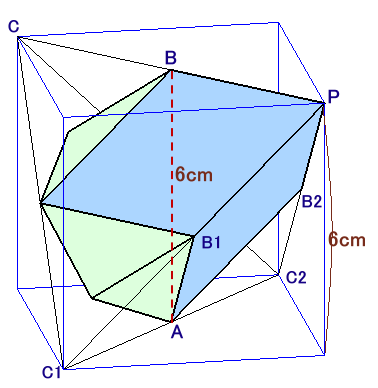
と求まります。なお、下図のように、大正四面体を立方体に埋め込むと、AB=6cmがちょうど立方体の1辺の長さに等しいことが分かります。(第131問解答例1)
すると、大正四面体は、この立方体から1辺の長さが6cmの直角二等辺三角形で高さ6cmの三角錐を4個除いたものとなっているので、
大正四面体の体積
=63−(1/3×1/2×62×6)×4
=72cm3
となります。以下、同様。
(その他の解法)
CADで描画して求める ・・・ kasamaさん、他