第426問の解答
問題[場合の数、平面図形]
|
|
|
|
|
|
ある円周上に、10個の点をとり、それらを結んで10角形を作ります。(注) (注)10個の点を結んでできる直線は10角形の辺も含めると45本ありますが、それらのうちどの2本を選んでも平行でなく、またどの3本を選んでも1点では交わらない(ただし、円周上を除く)ものとします。 |
|
|
|
|
|
解答例1
長野 美光さん、Taro さん、tomhさん、CRYING DOLPHINさん、アヒーのおじさんさん、姉小路さん、なかさん、小学名探偵さん、uchinyanさん、M.Hossieさん、kataさん、水田Xさん、他
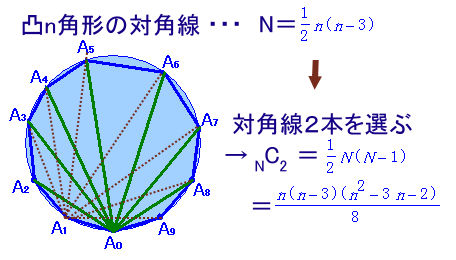
まず、対角線の本数を数えてみましょう。以下では、一般的に凸n角形として考えます。
一つの頂点について対角線を引けるのは、自分とその両隣を除く(n-3)個あります。
従って、全部でn(n-3)本引けますが、各対角線について両端の頂点で重複して数えていることになります。
よって、実際の本数は、この半分の
N=1/2×n(n-3)本
となります。従って、対角線2本を選ぶのは、全部で
NC2=1/2×N(N-1)=1/8×n(n-3)(n2-3n-2)通り
となります。題意より、どの対角線2本をとっても平行ではないので、必ず交点1個をもちます。
また、3本の対角線は1点では交わらないので、これらの頂点は全て異なるので、
交点数合計=1/8×n(n-3)(n2-3n-2)個
となります。(本問では、595個)
さて、対角線の交点がn角形のどこにできるかで分類してみましょう。
n角形の内側になる場合(第390問参照)
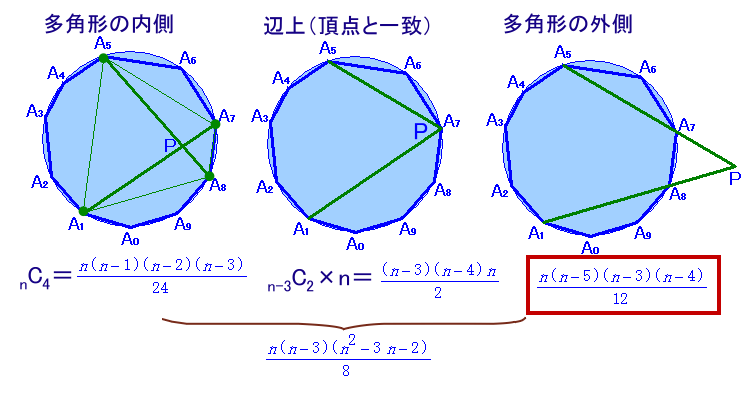
凸n角形の対角線の交点は、多角形の4個の頂点を選ぶとそれに対して1個の交点が対応します。
従って、
交点数=nC4=1/24×n(n-1)(n-2)(n-3)
と求まります。(本問では、210個)
n角形の辺上になる場合(いずれかの頂点と一致する)
この場合、対角線の交点は、いずれかの頂点と一致します。
各頂点を固定し、これが対角線の交点になる場合を考えてみましょう。
この場合、交点はこの頂点を通る(n-3)本の対角線から2本選ぶn-3C2個となります。従って、
交点数=n-3C2×n=1/2n(n-3)(n-4)個
となります。(本問では、210個)
n角形の外側になる場合(求める本数)
全体の交点数から、1.内側、2.辺上の交点数を除いて求めます。
交点数=1/8×n(n-3)(n2-3n-2)−1/24×n(n-1)(n-2)(n-3)−1/2(n-3)(n-4)n
=1/12×n(n-3)(n-4)(n-5)個
となります。(本問では、595−210−210=175個)従って、本問では、n=10として、
外側の交点数=1/12×10×7×6×5=175個
と求まります。答: 175個
以上
解答例2
mhayashiさん、uchinyanさん、スモークマンさん、他
解答例1では、n角形の内側にある交点数を、頂点4個を選んで求めました。
今度は、頂点4個を選ぶと外側に交点が2個できることに着目してみます。
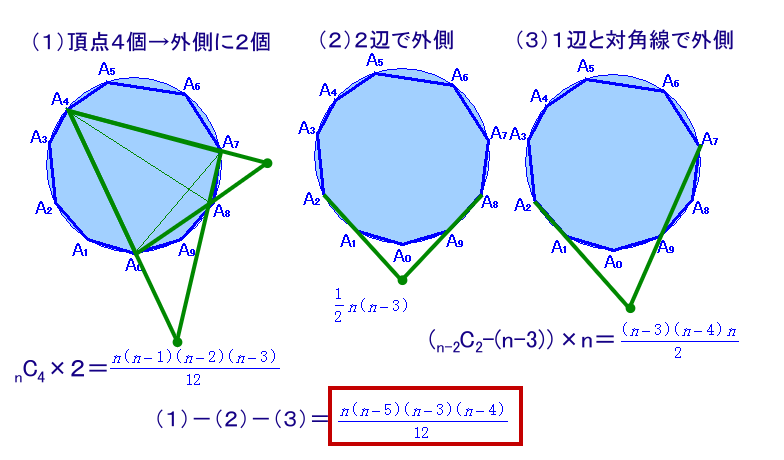
頂点4個を選んで外側にできる交点
頂点4個を選ぶと1個の凸四角形ができます。
このとき、隣り合わない2個ずつの頂点を結ぶと内側に1個交点ができます。
今度は、隣り合う2個ずつの頂点を選ぶと(選び方は2通り)外側に1個ずつ、
合計2個の交点ができます。従って、
交点数=nC4×2=1/12×n(n-1)(n-2)(n-3)個
となります。(本問では、420個)
2辺で外側にできる交点
辺を1本選ぶと、自分とその両隣を除く(n-3)本の辺とで交点が外側にできる。
従って、n(n-3)個の交点ができるが、2辺の選び方で重複して数えていることになるので、
交点数=1/2×n(n-3)個
となります。(本問では、35個)
1辺と対角線で外側にできる交点
1辺を固定して考えます。
最初の1辺に含まれる2頂点以外の(n-2)個の頂点から2個を選ぶと、もう一方の対角線が選べます。
ただし、このうち2頂点がn角形の辺となる場合の(n-3)通りは除く必要がありますので、
n-2C2−(n-3)=1/2×(n-3)(n-4)個
の頂点ができます。従って、1辺はn個あるので、
交点数=1/2×(n-3)(n-4)n個
となります。 (本問では、210個)従って、
求める交点数=(1)−(2)−(3)=1/12×n(n-3)(n-4)(n-5)個
となります。(本問では、420−35−210=175個)
解答例3
辻。さん、DrKさん、小学名探偵さん、nemuさん、みかんさん、エルクさん、N.Nishiさん、 他
ここでは、10角形に限定し考えることにします。
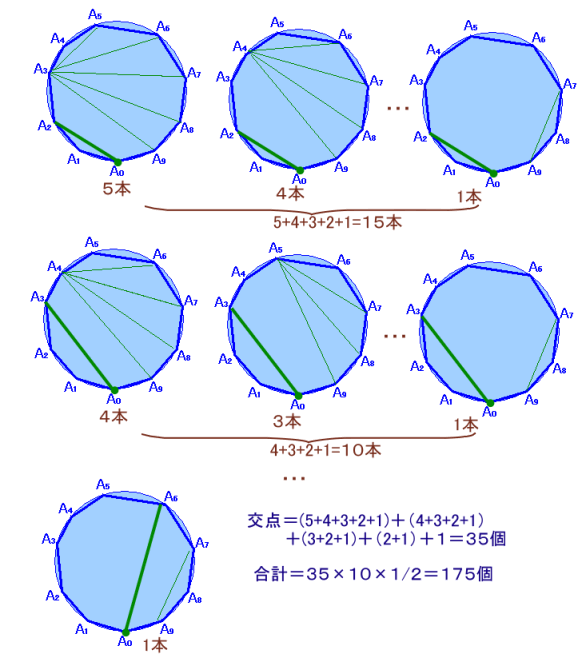
1頂点を固定し、そこから時計回りに頂点をA0、A1、・・・、A9とします。
A0と結んで対角線となる頂点は、A2、・・・、A8の7個になります。
それぞれの場合に分けて、これより右側に対角線が何本引けるかを数えていきます。
A2の場合
A3A5、A3A6、・・・、A3A9 ・・・ 5本
A4A6、A4A7、A4A8、A4A9 ・・・ 4本
A5A7、A5A8、A4A9 ・・・ 3本
A6A8、A6A9 ・・・ 2本
A7A9 ・・・ 1本
交点数=5+4+3+2+1=15個A3の場合
A4A6、A4A7、A4A8、A4A9 ・・・ 4本
A5A7、A5A8、A4A9 ・・・ 3本
A6A8、A6A9 ・・・ 2本
A7A9 ・・・ 1本
交点数=4+3+2+1=10個A4の場合
A5A7、A5A8、A4A9 ・・・ 3本
A6A8、A6A9 ・・・ 2本
A7A9 ・・・ 1本
交点数=3+2+1=6個A5の場合
A6A8、A6A9 ・・・ 2本
A7A9 ・・・ 1本
交点数=2+1=3個A6の場合
A7A9 ・・・ 1本
交点数=1個A7、A8場合 ・・・ 右側に対角線は引けない
よって、
合計=15+10+6+3+1=35個
となります。頂点は10個あるので、交点数は全部で35×2=350個となりますが、
2つの対角線について交点を重複して数えているので、
実際の交点数=350×1/2=175個
となります。
解答例4
Toru Fukatsuさん、uchinyanさん、ほげさん、 他
解答例3では力業で数えましたが、もう少しスマートに数えられないでしょうか。
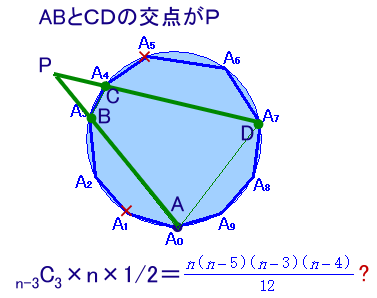
下図のように、一つの頂点Aを固定して、残りの頂点から3個選んでB、C、Dと、ABとCDの交点が1個外側にできます。
残りの頂点は(n-1)個ありますが、ABおよびCDが多角形の対角線となるためには、
BはAの右隣であってはならず、またDはCの右隣であってはいけません。従って、アバウトに考えると残りの頂点は(n-3)個から3個選ぶとしてもよさそうです。 ・・・ (1)
すると、この場合の数はn-3C3通りあるので、あとは解答例3と同様にして、
交点数=n-3C3×n×1/2=1/12×n(n-3)(n-4)(n-5)個
と求まります。(1)のところをもう少し厳密にするには、下記のように考えるといいでしょう。
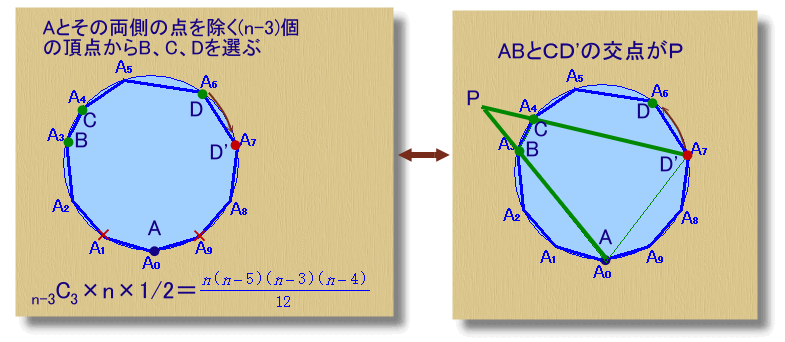
すなわち、Aとその両隣の点を除く(n-3)個の頂点から3個選んで、順にB、C、Dとします。(この選び方は、n-3C3通り)
このときDの右隣の頂点をD'とすると、DはAの左隣の頂点ではないので、D'はAよりは左側にある頂点となります。
こうすると、ABおよびCD'の間には別の頂点が存在するので、それぞれn角形の対角線となります。今度は、ABとCD'がn角形の対角線としましょう。
ABの間には別の頂点が存在するので、BはAの右隣の頂点ではありません。
また、CDの間には別の頂点が存在しますから、DをD'の左隣の頂点とすると、D'はCよりは右側にある頂点となります。
従って、B、C、Dは、Aと両隣の点を除く3つの頂点となります。上記の対応は1対1となるので、
ABとCD'がn角形の対角線となる場合の数
=Aとその両隣の点を除く(n-3)個の頂点から3個選ぶ選び方
=n-3C3通り
となります。以下、同様。
((1)の別解)
ABの距離(BがAより何番目の頂点かを数えたもの)をx、BCの距離をy、CDの距離をz、DAの距離をwとします。
x、y、z、wは
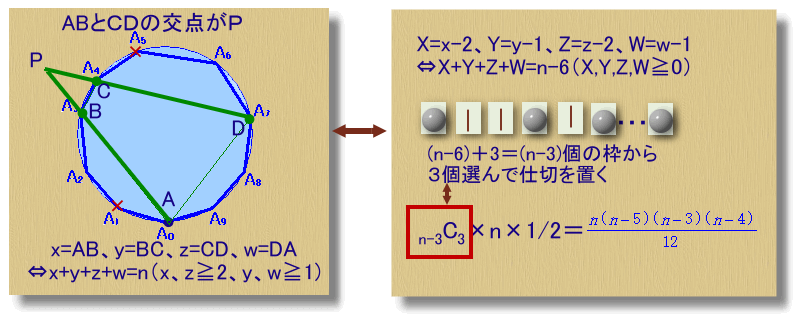
x+y+z+w=n(ただし、x≧2、y≧1、z≧2、w≧1) ・・・ (2)
を満たす整数となります。逆に(2)を満たすx、y、z、wに対して、Aから順にB、C、Dを決めていけば、
ABとCDはn角形の対角線となり、ABとCDの交点はn角形の外側にできます。従って、(2)を満たす整数解の個数を数えればいいことになります。
ここでは、(2)の替わりにX=x-1、Y=y-1、Z=z-1、W=w-1と置き換えて
X+Y+Z+W=n-6(ただし、X≧0、Y≧0、Z≧0、W≧0) ・・・ (3)
を考えてみましょう。この個数は、上記左図のように、(n-6)+3=(n-3)個の枠から3個選んで、それぞれに仕切を置く場合の数として求めることができます。仕切と仕切の間にある碁石の個数の和は(n-3)となり、碁石の個数は0以上となるからです。
従って、この場合の数は、n-3C3通りとなります。