第133問の解答
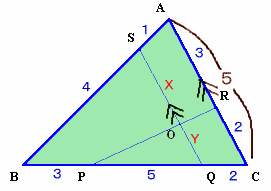
1.問題 [平面図形]
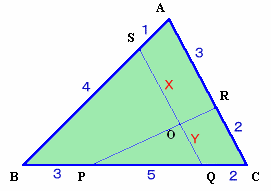 |
|
2.解答例1(Taroさん、他)
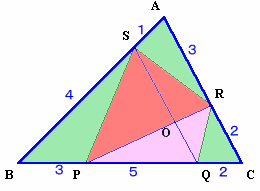
SO:OQ=△PSR:△PQRより求めます。
S=△ABCとします。
△PRC=S×PC/BC×CR/AC=S×7/10×2/5=S×7/25。
△PQR=△PRC×PQ/PC=S×7/25×5/7=S×5/25。四角形ABPR=△ABC−△PQR=S−S×7/25=S×18/25。
△SBP=S×BS/AB×BP/BC=S×4/5×3/10=S×6/25。
△SAR=S×SA/AB×AR/AC=S×1/5×3/5=S×3/25。
よって、△PSR=四角形ABPR−△SBP−△SAR
=S×18/25−S×6/25−S×3/25=S×9/25。従って、SO:OQ=△PSR:△PQR=S×9/25:S×5/25=9:5。
答:9:5
以上
3.解答例2(ありっちさん、長野美光さん、パリンさん、きょえぴさん、わかさひ君すーぱーさん、AUさん、DrKさん、うっしーさん、kakeruさん、他多数)
ACの長さを5とする。
BS:SA=BQ:QC=4:1より、△SBQと△ABCは相似、SQとACは平行。
SQ=AC×4/5=4。
OQ=RC×5/7=2×5/7=10/7。
従って、SO=SQ−OQ=4−10/7=18/7。
よって、SO:OQ=18/7:10/7=9:5。
4.解答例3(たなかさん、Gouさん、他)
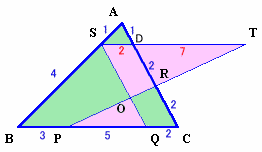
BRとSQの交点をTとする。
図1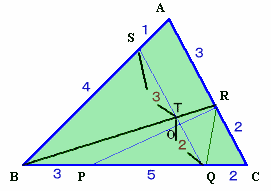 |
図2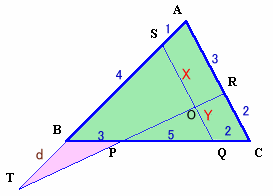 |
図1で、解答例2と同様にして、SQとACは平行、
よってST:TQ=AR:RC=3:2。△BTQにおいてメネラウスの定理より、
(QP/PB)*(BR/RT)*(TO/OQ)=1
よって、TO/OQ=(PB/QP)*(RT/BR)=3/5×1/5=3/25。TQを28とすると、TO=3、OQ=25。
ST=TQ×3/2=28×3/2=42。
よって、
SO=ST+TO=42+3=45、
OQ=TQ−TO=28−3=25。SO:OQ=45:25=9:5。
(別解)
図2で、ABの延長とRPの延長の交点をT、SB:BT=4:dとする。
△ABCとRTに関してメネラウスの定理により、
(AR/RC)*(CP/PB)*(BT/TA)=1
3/2*7/3*d/(d+5)=1
d/(d+5)=7/2
よって、d=2。また、△SBQとRTに関してメネラウスの定理により、
(SO/OQ)*(QP/PB)*(BT/TS)=1
(SO/OQ)*5/3*2/6=1
よって、SO/OQ=3/5*6/2=9/5、SO:OQ=9:5。
5.解答例4(香川仁志さん、他)
SからBCと平行に直線を引き、ABとの交点をD、PRの延長との交点をTとする。BCの長さを10として考える。
△ASDと△ABCは相似だから、
SD=BC×AS/AB=10×1/5=2。
AD=AC×1/5、
よって、
DR=AR−AD=AC×3/5−AC×1/5=AC×2/5=RC。△DTRと△CRPは相似だから、
DT=PC×DR/CR=7×2/2=7。△STOと△QPOは相似だから、
SO:OQ=ST:PQ=9:5。
6.解答例5(有無相生さん、しんご師匠さん、他)
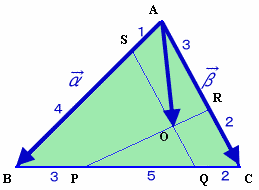
ベクトルで考えます。ベクトルABを→ABのように書くことにします。
→α=→AB、→β=→ACとします。
→AS=1/5→α、→AQ=1/5→α+4/5→β と表せるので、t=SO/SQとおくと、
→AO=(1-t)・→AS+t・→AQ
=(1-t)・1/5→α+t・(1/5→α+4/5→β)
=1/5→α+t・4/5→β ・・・ (1)→AR=3/5→β、→AP=7/10→α+3/10→β と表せるので、s=PO/PRとおくと、
→AO=(1-s)・→AP+s・→AR
=(1-s)・(7/10→α+3/10→β)+s・3/5→β
=(1-s)・7/10→α+(1+s)・3/10→β ・・・ (2)(1)、(2)より、
1/5=(1-s)・7/10、t・4/5=(1+s)・3/10
これを解いて、s=5/7、t=9/14を得る。よって、SO:SQ=9:5となります。