第１３７問の解答

１．問題　［場合の数、最短距離］

問題図

　左図のように、長さの等しい２４本のひごを使って組み立てられた立体があります。
　このひごをたどってＰからＱまで遠回りをせずに進むとき、その通り方は全部で何通りありますか？

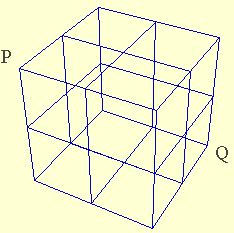２．解答例１［数え上げ］(溝部光洋さん、うっしーさん、シイサンさん、長野美光さん、他)

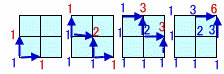
１面だけだと数え上げも比較的簡単で、６通りあることが分かります。

参考図1

でも、経路数が多いときや、本問のように立体になると、数え間違いが生じてきます。

そこで、次のような各格子点を通過する場合の数を数えていく方法にすると、確実です。

参考図2

まず、出発点では１通りです。
次の格子点では、最初の点からの経路しかないので、やはり１通り。

さらに、次の点のうち、頂点まではあいかわらず経路は１本で１通り、
真ん中の点は２個所から合流するので１＋１＝２通り。
次の点では、頂点からと真ん中からが合流するので、１＋２＝３通り。
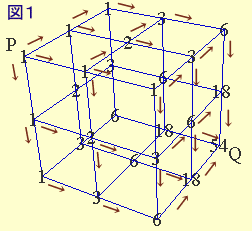
最後の点では、２個所から合流し、３＋３＝６通りとなります。

同様に、本問では、Ｐを含む３つの面は、上記同様に計算できます。

参考図3

Ｐを含まない面の中央の格子点では、３＋３＝６通り、
Ｑの１歩手前の点では、６＋６＋６＝１８通り、
Ｑでは、１８＋１８＋１８＝５４通りとなります。		 （参考）マウスでドラッグして下さい。
(Sキーをおすと、ステレオ画像になります)

答：５４通り

以上

３．解答例２［順列・組み合わせによる計算１］
(ταροさん、杉本未来さん、長野美光さん、トトロ＠Ｎさん、むらかみさん、ｏkaokaさん、有無相生さん、井合宗太郎さん、他多数)

平面の場合、一般に縦ｍ×横ｎの最短経路はm+nＣmになります。（参考）

参考図4

従って、２×２のときは、4Ｃ2＝4!/(2!・2!)=4・3・2・1/(2・1・2・1)=6通り。

もし、立体の中央の点も通ること許すと、２×２×２の最短経路となります。そこで、この数え方を、次のように考えます。

３方向×２＝６個の進む方向を並べ替える６!通りの経路で、各方向については２個の進む方向の並べ替え２!通りが重複しているため、求める経路数は、
　　　　６!／（２!・２!・２!）
　　＝６・５・４・３・２・１／（２・１・２・１・２・１）
　　＝９０通り
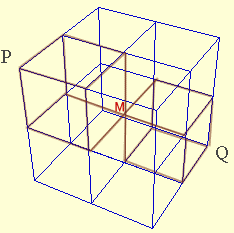
となります。

この中で、中央の点Ｍを通る最短経路は、下図のようにＰ→Ｍ、Ｍ→Ｑの１×１×１が２回の最短経路となるので、３!/(１!・1!・1!）＝６通りの２乗、すなわち６×６＝３６通りあります。

参考図5

よって、求める経路数は、９０−３６＝５４通りとなります。

４．解答例３［順列・組み合わせによる計算２］(中村明海さん、他)


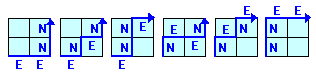
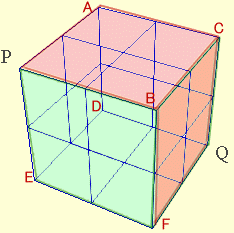
Ｐ、Ｑを含まない辺の中点は、下図のようにA、B、C、D、E、Fの６個所あります。

参考図6

Ｐ →Ａ→Ｑは、それぞれ２×１の最短経路なので３!/（２!・１!）＝３通りの２乗、すなわち３×３＝９通りあります。
Ｐ→Ｂ→Ｑ、・・・、Ｐ→Ｆ→Ｑも同様に９通りなので、
合計９×６＝５４通りとなります。

５．解答例４［順列・組み合わせによる計算３］(大岡敏幸さん、他)


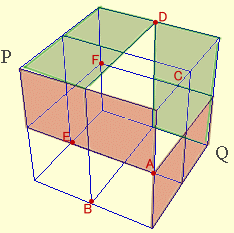
Ｐ→Ｑの最短経路は、Ｐを含む３つの面（PACB、PADE、PBFE）と、Ｑを含む３つの面（QFBC、QFED、QDAC）のうち、それぞれ１面ずつを通ることになります。

参考図7

面の選び方は、3C1×3C1＝９通りありますが、そのうち共通点を含まない、相対する２面の組み合わせの３通りを除くと合計６通りになります。

それぞれは、例えばPACBとQFBCならＰＡＱＦの４×２の最短経路となるので、６!/（４!・２!）＝６・５・４・３・２・１／（４・３・２・１・２・１）＝１５通り。
合計１５×６＝９０通りになります。

ただし、これらの中には上記（PACBとQFBC）および（PBFEとQFBC）のように各面を共通とする組み合わせ６通りが含まれます。
この場合、Ｐ→Ｂ→Ｑの経路（Ｐ→Ｂは１通り、Ｂ→Ｑは２×２の最短経路＝６通り）は重複して数えています。

従って、合計６×６＝３６通りが重複して数えていることになるので、
結局求める最短経路数は、９０−３６＝５４通りとなります。