第147問の解答
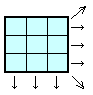
1.問題 [整数の性質、魔方陣]
 |
|
2.解答例1(清川育男さん、杉本未来さん、AUさん、すうぱあさん、きょえぴさん、トトロ@Nさん、ありっちさん、中村明海さん、有無相生さん、Nagahiroさん、N.Nishiさん、mhayashiさん、あまれっとさん、他多数)
各マスに入る数字をa、b、c、・・、iとし、全ての積をS、1列の積をsとします。
abcdefghi=(abc)(def)(ghi)=s3=S、
s=S1/3 ・・・ (1)、
よって、sを最小にするためには、Sを最小にすればいいことがわかる。ここで、a、b、c、・・、iに入っている素因数をp、q、r、・・・、tとし、
a=pa1qa2ra3・・tan、b=pb1qb2rb3・・tbn、・・、i=pi1qi2ri3・・tin、
および、s=ps1qs2rs3・・tsnとします。abc=pa1+b1+c1qa2+b2+c2ra3+b3+b3・・tan+bn+cn=ps1qs2rs3・・tsn、
よって、a1+b1+c1=s1、a2+b2+c2=s2、a3+b3+b3=s3、・・、an+bn+cn=sn。
同様に、d1+e1+f1=s1、d2+e2+f2=s2、d3+e3+f3=s3、・・、dn+en+fn=sn、
および、d1+e1+f1=s1、d2+e2+f2=s2、d3+e3+f3=s3、・・、dn+en+fn=sn。全く同様にして、縦、斜め方向にも同じことがいえるので、
・・・(2)
のような関係が成り立つ。
ここで、r=・・・=t=1、またはq=・・・=t=1としても、題意が成り立つので、sを最小にするには、素因数が1個または2個の場合に限る。
しかも素因数の値にかかわらず、(2)が成り立てば題意が満たされるので、
・素因数が1個のとき:p=2
・素因数が1個のとき:p=2、q=3
のいずれかの場合となることが分かる。(1)素因数が1個のとき:
(2)より、a1、b1、c1、・・、i1は縦、横、斜めの和が全てs1に等しく、また全て値は異なる(たとえば、a1=b1とすれば、a=2a1=b=2b1となって題意に反する)0以上の整数であることから、いわゆる魔方陣となっていることが分かる。
sを最小にするには、a1、b1、c1、・・、i1は0から8の整数であればOK。
(1)、(2)より、s1=S1/3 ・・・ (3)(ただし、S1=a1+b1+・・+i1)となるので、
s1=(0+1+・・+8)/3=(8・9/2)/=3=12
よって、s=212=4096となります。具体的な例としては、次のようなものがあります。(参考:算チャレ第206問)

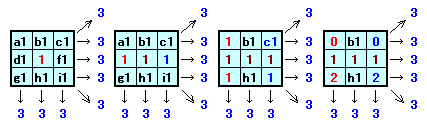
(2)素因数が2個のとき:
素因数が1個のときと異なるのは、a1、b1、c1、・・、i1、およびa2、b2、c2、・・、i2は全て異なる必要はない。
ここで、
(a1+e1+i1)+(c1+e1+g1)+(b1+e1+h1)+(d1+e1+f1)=4s1
(a1+b1+c1+d1+e1+f1+g1+h1+i1)+3e1=4s1
3s1+3e1=4s1
よって、e1=s1/3がなりたつ。
全く同様に、e2=s2/3。 ・・・ (4)すなわち、s1、s2は3の倍数となり、
いずれかが0の場合は、
a1=b1=c1=・・=i1=0またはa2=b2=c2=・・=i2=0
となり、素因数が2個であることに反する。従って、s1、s2は3以上。
もし、s1=s2=3となるものがみつかれば、それが最小となる。・・・(5)
・・・(6)
上表のように、各列に0、1、2を配置し、縦、横、斜めに必ずこの3つの整数が来るように並べ(ラテン方陣という)、素因数2のラテン方陣と素因数3のラテン方陣の各マスの組み合わせ(オイラー方陣という)が異なるようにすれば、掛け合わせたものは題意を満たす魔方陣になる。
このとき、s=(2×3)3=63=216となります。
ちょうど、これは36の約数が2n×3m(n=0,1,2、m=0,1,2)のちょうど3×3=9通りの整数あるることに対応しています。
素因数1個の場合の4096より、素因数2個の場合の216のほうが小さいので、216が最小になります。
答:216
以上
3.解答例2(ふきゅさん、数楽者さん、他)
解答例1の(2)素因数が2個のときの3×3のオイラー方陣を3進数表現を使って次のように求めることが出来ます。
まず、1から9を使った3×3の魔方陣で各マスの数字から1を引いて、0から8を使った魔方陣とします。
次に、これらの数字を3進数表現に変換します。
さらに、各マスの数字を第2位の数字と第1位の数字に分解します。
すると、ちょうど解答例1の(6)を反時計回りに90度回転したものが得られます。
(参考)解の魔方陣が対象なものを除いて唯一であること
解答例1の(2)素因数が2個のときのa1、b1、c1、・・、i1を求めてみましょう。
(4)、(5)から、e1=1、s1=3が得られています。
a1+1+i1=3より、0≦a1、i1≦2。同様に、残りの数字も0、1、2のいずれかになります。
いま、d1=1と仮定すると、d1+1+f1=3よりf1=1。
さらに、a1=1と仮定すると、a1+1+g1=a1+1+r1=3より、g1=r1=1となり、残りも全て1になるので不適。
よって、a1=0または2。a1=0とします。
a1+1+g1=a1+1+r1=3より、g1=r1=2となり不適。
同様に、a1=2とすると、g1=r1=0、h1=3となり不適。従って、d1=0または2となります。
d1=0とすると、f1=2となります。
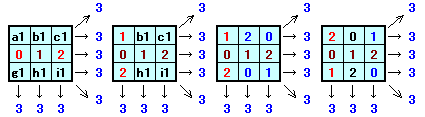
a1=0とすると、g1=3となるので不適。
よって、a1=1または2。a1=1とすると、g1=2、i1=1。
残りは、h1=0、c1=0、b1=2となります。(ケースa)
a1=2とすると、g1=1、i1=0。
残りは、h1=2、c1=1、b1=0となります。(ケースb)d1=2と仮定するとしても、同様にケースc、ケースdが得られます。
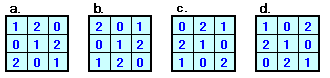
以上4ケースは、対象性を除くと同じパターンのラテン方陣になっています。
全く同様に、a2、b2、c2、・・、i2も上記4ケースのラテン方陣になります。
さて、a1、b1、c1、・・、i1がケースaでa2、b2、c2、・・、i2がケースbの場合を(a,b)のように表すとすれば、
各マスの数字の組み合わせに同じものがないようにする必要があるので、
(a,b)、(a,c)、(b,a)、(b,d)、(c,a)、(c,d)、(d,b)、(d,a)の6通りになります。いずれの場合も、結果的には36の9つある約数を各マスに並べたものになるので、対象性を除くと同一とみなすことができます。