第９１問の解答

１．問題　［場合の数・カタラン数］

問題図
　多角形を対角線で区切り、３角形に分割することを考えます。このとき対角線どうしは互いに交わらないように引きます。すると、４角形は左図のように２通り、５角形は５通りの分け方があります。

では、６角形の場合は何通りの分け方があるでしょうか？

２．解答例１（PYQさん他）

ｎ角形を３角形に分割する分け方の数（分割数と呼びます）をE(n)とします。
E(2)=1、E(3)=1、E(4)=4、E(5)=5までは分かっています。

また、６角形の頂点をＰ１、Ｐ２、・・・Ｐ６とします。

６角形を３角形で分割したとき、各辺は必ずどれかの３角形の１辺となるので、辺Ｐ１Ｐ２を１辺とする３角形に着目して分類します。

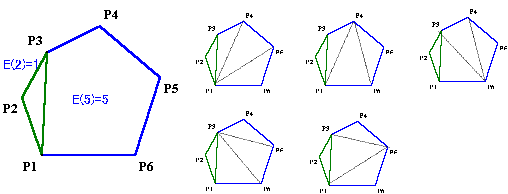
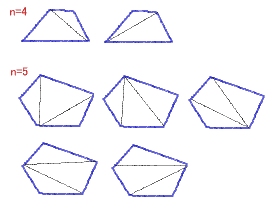
Ｐ３のとき（５通り）
参考図１
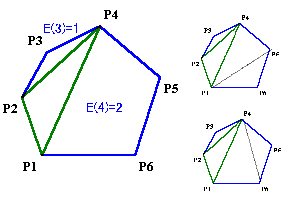
Ｐ４のとき（２通り）
参考図２
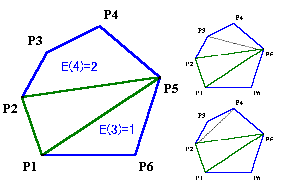
Ｐ５のとき（２通り）
参考図３
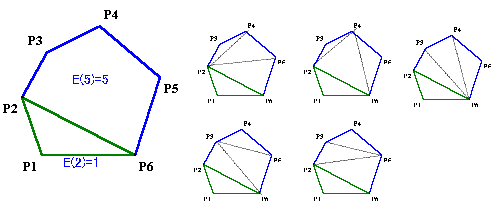
Ｐ６のとき（５通り）
参考図４

　すると、Ｐ１、Ｐ２以外の頂点はＰ３、Ｐ４、Ｐ５、Ｐ６のいずれかとなり、それぞれ三角形Ｐ１Ｐ２Ｐm（３≦ｍ≦６）の左側の多角形の分割数と右側の多角形の分割数の積となる。

従って、E(6)=E(2)・E(5)+E(3)・E(4)+E(4)・E(3)+E(5)・E(2)
　　　　　　=1×5+1×2+2×1+5×1=14通りとなります。

答：１４通り

以上

３．解答例２：一般解（カタラン数）

カタラン数については、「算数チャレンジャーに挑戦！」第６問でも取り上げています。
縦ｎ×横ｎの格子上を対角線より右側へは行かないように進むときの最短経路数をＨ（ｎ）とすると、Ｈ（ｎ）＝2nCn/(n+1)となります。

参考図６　

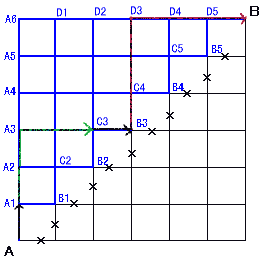
実は、Ｅ（ｎ）＝Ｋ（ｎ−２）が成り立ちます。（補題）

この事実を用いると、Ｅ（６）＝Ｋ（４）＝8C4/(4+1)=(8・７・６・５)/(４・３・２・１・５)＝１４通りと分かります。

（補題の証明）

上図よりＫ（６）を考えてみると、都合上Ｋ（０）＝１として、

Ｋ（６）＝ 　Ｋ（０）・Ｋ（５）　 ・・・ B1を通る場合
（A・A1・B1→B1からBへの制限付き最短経路）
＋Ｋ（１）・Ｋ（４） ・・・ B1を通らず、B2を通る場合
（A・A1→A1からC2への制限付き最短経路→C2・B2→B2からＢへの制限付き最短経路）
＋Ｋ（２）・Ｋ（３） ・・・　 B1、B2を通らず、B3を通る場合
（A・A1→A1からC3への制限付き最短経路→C3・B3→B3からＢへの制限付き最短経路）　
＋Ｋ（３）・Ｋ（２） ・・・　 B1、B2、B3を通らず、B4を通る場合
（A・A1→A1からC4への制限付き最短経路→C4・B4→B4からＢへの制限付き最短経路）　
＋Ｋ（４）・Ｋ（１） ・・・　 B1、B2、B3、B4を通らず、B5を通る場合
（A・A1→A1からC5への制限付き最短経路→C5・B5→B5からＢへの制限付き最短経路）　
＋Ｋ（５）・Ｋ（０）　 ・・・　 B1、B2、B3、B4、B5を通らず、B6を通る場合
（A・A1→A1からD5への制限付き最短経路→D5・B）　

という漸化式が導かれます。

一般に、K(n)=K(0)・K(n-1)+K(1)・K(n-2)+・・・+K(n-2)・K(1)+K(n-1)・K(0)となります。
　　　　　　　　
さて、E(n)=K(n-2)を帰納法で示すことにします。
１）n=2のとき、E(2)=1、K(0)=1よりE(n)=K(n-2)が成り立つ

２）n≦m-1(m≦3)で成り立つとします。
　　n=mのとき、
　　　E(n)=E(2)・E(n-1)+E(3)・E(n-2)+・・・+E(n-2)・E(3)+E(n-1)・E(2)
　　　　　=K(0)・K(n-3)+K(1)・K(n-4)+・・・+K(n-4)・K(1)+K(n-2)・K(0)
　　　　　=K(n-2)

以上から、帰納法によりE(n)=K(n-2)が示された。