第１０７問の解答

問題［規則性]

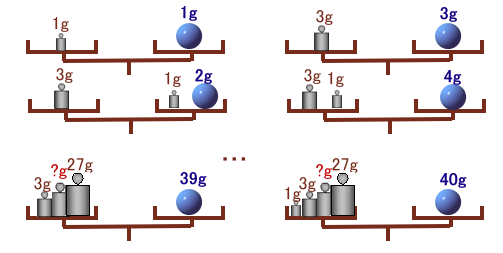
天秤(てんびん)を使って１g、２g、３g、・・・ 、４０gと、１gきざみで４０gまで量れるようにします。
分銅は４個まで使うことができて、分銅を左右両方の皿に載せても構いません。
今、手元に１g、３g、２７gの３つの分銅があるとき、あともう１個は何gの分銅があれば良いでしょう？

解答例１[最大40gを量るのは一方に全部乗せ]

ゴンともさん、龍さん、そうたさん、りかさん、HAJIさん、 さび＾＾＾さん、NS-HIGASHIさん、A.NOUCHIさん、不思議草さん、他

まず、４個の分銅で何通りの重さが量れるかを考えてみましょう。

参考図１

各分銅に対して、

  1. 左の皿に載せる

  2. 右の皿に載せる

  3. どちらにも載せない

の３通りがあります。

従って、４個の分銅では、合計３4＝８１通りになりますが、
このうちどの分銅も皿に載せない１通りは重さを量らないので除外します。

また、左右に載せた分銅を入れ替えても同じ重さを量ることになるので、
半分の（８１−１）÷２＝４０通りになります。

さて、このうち最大の重さは、片方の皿に４個の分銅を載せた場合なので、
　１g＋３g＋？g＋２７g＝４０g

よって、残る１個の分銅は９gになります。

なお、１g、３g、９g、２７gの４個の分銅で１g〜４０ｇまで１ｇきざみで量ることができる
ということについては解答例２で考えましょう。

答　 ９g

以上

解答例２[１,３,□,２７だから９ 、５ｇを量るのに要る分銅、３進法]

綾巳さん、らいおんさん、こういちさん、yyさん、パリンさん、 ミト清さん、パァ〜子さん、kasamaさん、あすさん、土橋　雅樹さん、 スマイルさん、あまれっとさん、多佳子さん、優太さん、かず。さん、 名無しさんさん、きょろ文さん、木村洋文さん、デールさん、ハラギャーテイさん、kobaさん、他

分銅を１個ずつ増やしながら考えます。

参考図２

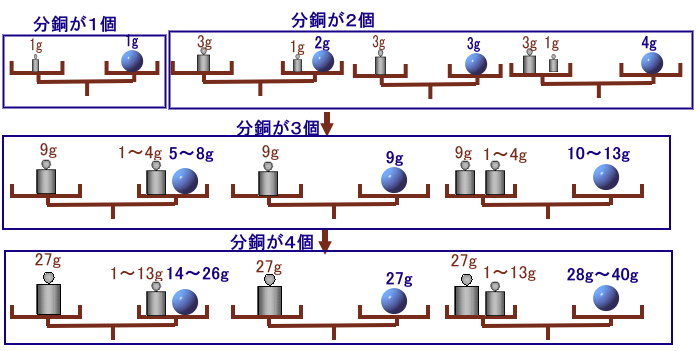
  1. 分銅が１gのとき　・・・　１g

  2. 分銅が１g、３gのとき　
    ・３gを左の皿、１ｇを右の皿に　・・・　２ｇ
    ・３g    を左の皿　　　　　　　　　　・・・　３ｇ
    ・３g    と１ｇを左の皿　　　　　　　　・・・　４ｇ

  3. 分銅が１g、３g、９gのとき　
    ・９gを左の皿、１〜４ｇを右の皿に　・・・　５〜８ｇ
    ・９g    を左の皿　　　　　　　　　　　　・・・　９ｇ
    ・９g    と１〜４ｇを左の皿　　　　　　　・・・　１０〜１３ｇ

  4. 分銅が１g、３g、９g、２７ｇのとき　
    ・２７gを左の皿、１〜１３ｇを右の皿に　・・・　１４〜２６ｇ
    ・２７g    を左の皿　　　　　　　　　　　　　・・・　２７ｇ
    ・２７g    と１〜１３ｇを左の皿　　　　　　　・・・　２８〜４０ｇ

となり、１ｇ〜４０ｇの４０通りが量れることが分かります。

（参考）一般に、１g、３g、３2g、・・、３ngのn個の分銅で、１g〜（３n−１）/２gを量ることができます。
　　　　・・・　「算数チャレンジャーに挑戦」第２問