第2問(1)の解答
1.問題
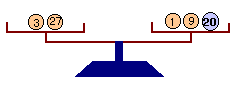
| (1)7個のおもりがあります。重さは、1g、3g、9g、27g、81g、243g、729gです。天秤とこれらのおもりを利用して1gから1093gまでの連続した整数に対する重さの全てをはかることができます。このことを説明して下さい。 (2)777gをはかるには、天秤におもりをどのように載せればよいでしょうか |
2.設問(1):解答例1(三好知之さん他)
帰納法的に考えてみましょう。
・おもりが1個のとき:1gを量ることができます。
・おもりが2個になったとき:2〜4gを量ることができます。
1gを右に載せることで3−1=2gを量ることができる。
3gを量ることができる。
1gを左に載せることで3+1=4gを量ることができる。
・おもりが3個になったとき:5〜13gを量ることができる。・1〜4gまでの量り方と逆の載せ方にし、9gを左に載せる。
9−4=5g〜9−1=8gを量ることができる。
・9gを左に載せる。
9gを量ることができる。
・1〜4gまでの量り方と同じにし、9gを左に載せる。
9+1=10g〜9+4=13gを量ることができる。・おもりが4個になったとき:14〜40gを量ることができる。
・1〜13gまでの量り方と逆の載せ方にし、27gを左に載せる。
27−13=14g〜27−1=26gを量ることができる。
・27gを左に載せる。
27gを量ることができる。
・1〜13gまでの量り方と同じにし、27gを左に載せる。
27+1=28g〜27+13=40gを量ることができる。・おもりが5個になったとき:41〜121gを量ることができる。
・1〜40gまでの量り方と逆の載せ方にし、81gを左に載せる。
81−40=41g〜81−1=80gを量ることができる。
・81gを左に載せる。
81gを量ることができる。
・1〜40gまでの量り方と同じにし、81gを左に載せる。
81+1=82g〜81+40=121gを量ることができる。・おもりが6個になったとき:122〜364gを量ることができる。
・1〜121gまでの量り方と逆の載せ方にし、243gを左に載せる。
243−121=122g〜243−1=242gを量ることができる。
・243gを左に載せる。
243gを量ることができる。
・1〜121gまでの量り方と同じにし、243gを左に載せる。
243+1=244g〜243+121=364gを量ることができる。・おもりが7個になったとき:365〜1093gを量ることができる。
・1〜364gまでの量り方と逆の載せ方にし、729gを左に載せる。
729−364=365g〜729−1=728gを量ることができる。
・729gを左に載せる。
729gを量ることができる。
・1〜364gまでの量り方と同じにし、729gを左に載せる。
729+1=730g〜729+364=1093gを量ることができる。
以上
3.設問(1):解答例2(中村明海さんによる)
| (補題) 1≦X≦1093に対して、 X=A0+A1×31+A2×32+A3×33+A4×34+A5×35+A6×36 と表せる。ただし、A0、・・、A6=−1,0,1のいづれかとする。 |
X1=1+1×31+1×32+1×33+1×34+1×35+1×36=1093、
X2=2+2×31+2×32+2×33+2×34+2×35+2×36=2096とおく。Y=X+X1とすると、1094≦Y≦X2となる。
Yを3進数で表し、
Y=B0+B1×31+B2×32+B3×33+B4×34+B5×35+B6×36
とする。ただし、B0、・・、B6=0,1,2である。このとき、
X=Y-X1
=(B0+B1×31+B2×32+B3×33+B4×34+B5×35+B6×36)−
(1 +1×31 +1×32 +1×33 +1×34 +1×35 +1×36)
=((B0-1)+(B1-1)×31+(B2−1)×32+(B3−1)×33+(B4−1)×34+(B5−1)×35+B6×36)よって、A0=B0-1、・・、A6=B6-1とおけば、A0、・・、A6=−1,0,1となり、
X=A0+A1×31+A2×32+A3×33+A4×34+A5×35+A6×36
となる。(補題の証明終わり)
さて、1≦X≦1093に対して、補題より
X=A0+A1×31+A2×32+A3×33+A4×34+A5×35+A6×36
と表せる。ただし、A0、・・、A6=−1,0,1のいづれか。このとき、0≦n≦6に対して、Anが
−1であれば3nのおもりを左の天秤に載せる、
0であれば3nのおもりはどの天秤にも載せない、
+1であれば3nのおもりを左の天秤に載せる
ことにすれば、Xgを量ることができる。以上
解答のページ(2)へ