問題(平面図形)
|
|
|
|
|
|
|
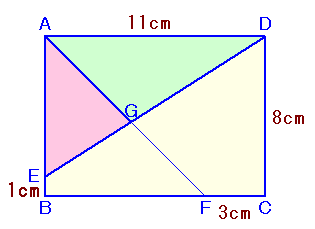 |
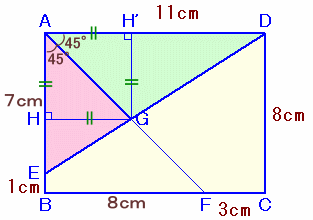
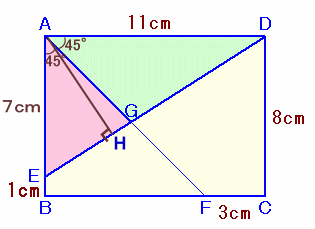
左図でABCDは長方形です。 △AEGと△ADGの面積の比を、最も簡単な整数の比として表わしなさい。 |
|
|
|
|
|
|
解答例1[AE:AD(高さが等しい) ]
| Banyanyanさん、ながちゃんさん、永嶋 幸司さん、ふじさきたつみさん、mhayashiさん、 ほなみさん、長野美光さん、文花さん、有無相生さん、信三さん、 tomhさん、まるケンさん、数楽者さん、マッスルさん、わにがわさん、 あまれっとさん、きょえぴさん、Feroさん、mkuraさん、TOMOKIさん、 USKさん、大岡 敏幸さん、とらいしくるさん、算数題魔人さん、 まこさん、 他 |
Gから辺AB、ADに下ろした垂線の足をそれぞれH、H'とします。
AE=AB−EB=8−1=7cm。
BF=BC−FC=11−3=8cm、
従って、AB=BF=8cm。よって、△ABFは、AB=BFの二等辺三角形となるので、
∠BAF=∠DAF=45°。従って、GH=AH=GH'。
△AEG=1/2×AE×HG、△ADG=1/2×AD×H'Gより、
△AEG:△ADG=AE:AD=7:11。答 7:11
以上
解答例2[AFとDCを延長して ]
| maruhagedonさん、辻。さん、ヌオさん、N.Nishiさん、スモークマンさん、 Nの悲劇さん、智ベン和歌山さん、トトロ@Nさん、美登利さん、ひろひでさん、 航介さん、他 |
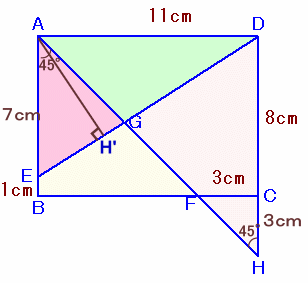
AFとDCの延長線の交点をHとし、AからDEに下ろした垂線の足をH'とします。
解答例1同様に∠BAF=45°を得るから、∠DHA=∠BAF=45°。
よって、DH=AD=11cm。△AEG=1/2×EG×AH'、△ADG=1/2×GD×AH'より、
△AEG:△ADG=EG:GD ・・・ (1)ABとDHは平行より、△AGEと△HGDは相似、
よって、EG:GD=AE:HD=7:11 ・・・ (2)(1)、(2)より、△AEG:△ADG=7:11。
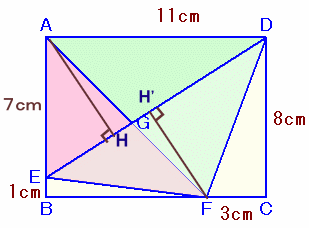
解答例3[△AEG:△ADG=△AEF:△ADF ]
| TORAさん、Taroさん、ミミズクはくず耳さん、勝浦捨てる造さん、HEROさん、 AIRさん、 他 |
解答例2と同様にして、△AEG:△ADG=EG:GD ・・・ (1)
また、これと同様に、△FEG:△FDG=EG:GD ・・・ (2)(1)、(2)より、
△AEF:△ADF
=(△AEG+△FEG):(△ADG+△FDG)
=EG:GD ・・・ (3)△AEF=1/2×AE×BF=1/2×7×8
△ADF=1/2×AD×CD=1/2×11×8、
よって、△AEF:△ADF=7:11 ・・・ (4)(1)、(3)、(4)より、
△AEG:△ADG=EG:GD=△AEF:△ADF=7:11
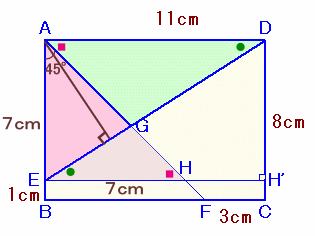
解答例4[△AEG:△ADG=EG:GD=EH:AD ]
| GROMITさん、HAJIさん、修平さん、MIKIちゃんさん、他 |
Eを通りBCと平行な直線を引き、AFとの交点をHとします。
解答例2と同様にして、△AEG:△ADG=EG:GD ・・・ (1)
△AEHは直角二等辺三角形だから、EH=AE=7cm。
ADとEHが平行より、△GEHと△GDAは相似、
よって、EG:GD=EH:AD=7:11 ・・・ (2)(1)、(2)より、△AEG:△ADG=EG:GD=7:11
解答例5[角の二等分線の定理を使って]
| ねこやんさん、hayatoさん、他 |
解答例1、2と同様に、
∠EAG=∠DAG=45° ・・・ (1)
△AEG:△ADG=EG:GD ・・・ (2)従って、三角形の角の二等分線に関する公式より、
EG:GD=AE:AD=7:11 ・・・ (3)。(2)、(3)より、
△AEG:△ADG=EG:GD=7:11