第1問(1)の解答
1.問題
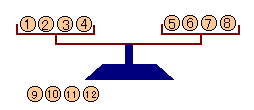
| (1)12個のおもりがあります。このうち、1個だけ他のおもりと重さが異なるものがあります。天秤を利用して何回かおもりを量り、どのおもりが他と異なるかを見つけて下さい。 さて、おもりを量る回数をできるだけ少なくするとして、最大何回量ればいいでしょうか。 また、その具体的な量り方を考えて下さい。 (2)7回まで量ることができるとします。このとき、最大何個のおもりのなから1個だけある重さの異なるものを見つけることができるでしょうか。 |
2.設問(1)
(おもりが12個の場合)
以下の方法で3回はかれば判定できます。
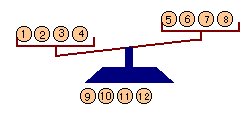
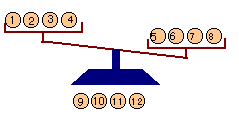
・1回目:1、2,3,4のおもりを左、5,6,7,8のおもりを右に載せます。
1.左が重いとき
1,2,3,4のどれかが重いか、
5,6,7,8のどれかがが軽い、
9,10,11,12は正しいと分かります。
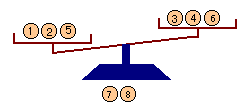
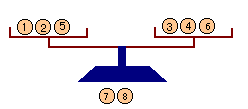
・2回目:1,2,5を左、3,4,6を右に載せます。
・左が重い
1,2のどれかが重いか、6が軽い、
残りは正しいと分かります。→
・3回目:1を左、2を右に載せます。 ・左が重い→1が重い
・釣り合う→6が軽い
・右が重い→2が軽い
・釣り合う
7,8のどれかが軽い、
残りは正しいと分かります。→
・3回目:7を左、8を右に載せます。 ・左が重い→8が軽い
・釣り合う→なし
・右が重い→7が軽い
・右が重い
3,4のどれかが重いか、5が軽い、
残りは正しいと分かります。→
・3回目:3を左、4を右に載せます。 ・左が重い→3が重い
・釣り合う→5が軽い
・右が重い→4が重い
2.釣り合うとき
1,2,3,4,5,6,7,8は正しく、
9,10,11,12のどれかが異なると分かります。
・2回目:9を左、10を右に載せます。
以下、4個の場合と同様
3.右が重いとき
1,2,3,4のどれかが軽いか、
5,6,7,8のどれかがが重い、
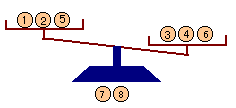
9,10,11,12は正しいと分かります。・2回目:1,2,5を左、3,4,6を右に載せます。
・左が重い
3,4のどれかが軽いか、5が重い、
残りは正しいと分かります。→
・3回目:3を左、4を右に載せます。 ・左が重い→4が軽い
・釣り合う→5が重い
・右が重い→3が軽い
・釣り合う
7,8のどれかが重い、
残りは正しいと分かります。→
・3回目:7を左、8を右に載せます。 ・左が重い→7が重い
・釣り合う→なし
・右が重い→8が重い
・右が重い
1,2のどれかが軽いか、6が重い、
残りは正しいと分かります。→
・3回目:1を左、2を右に載せます。 ・左が重い→2が軽い
・釣り合う→6が重い
・右が重い→1が軽い
以上
(おもりが13個の場合)
実は、3回で判定できるおもりの最大個数は13個です。これは、2回目以降では正しいおもりを利用できるのを12個の場合では使わなかったためです。
判定方法は、12個の場合同様4個ずつ天秤に載せ、9,10,11,12,13の5個を残します。
天秤がどちらかに傾いた場合は12個の場合と全く同様に判定できます。
・釣り合った場合:9,10,11,12,13のどれかが異なり、その他は正しいと分かります。
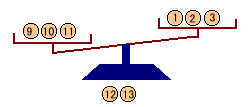
9,10,11を左に、正しい1,2,3を右に載せます。
・左が重い
9,10,11のどれかが重い、
残りは正しいと分かります。→
・3回目:9を左、10を右に載せます。 ・左が重い→9が重い
・釣り合う→11が重い
・右が重い→10が重い
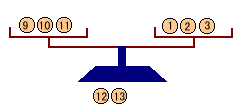
・釣り合う
12,13のどれかが異なる、
残りは正しいと分かります。→
・3回目:12を左、1を右に載せます。 ・左が重い→12が重い
・釣り合う→13が異なる
・右が重い→12が軽い
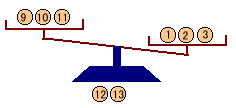
・右が重い
9,10,11のどれかが軽い、
残りは正しいと分かります。→
・3回目:9を左、10を右に載せます。 ・左が重い→10が軽い
・釣り合う→11が軽い
・右が重い→9が軽い
以上
解答のページ(2)へ