第２９問の解答

１．問題

問題図
左図のように△ＡＢＣの各辺を１：３に内分する点をＤ、Ｅ、Ｆとします。
また、ＡＥ、ＢＦ、ＣＤ、の交点をＰ、Ｑ、Ｒとします。

△ＰＱＲの面積と△ＡＢＣの面積の比はいくらになるでしょうか。

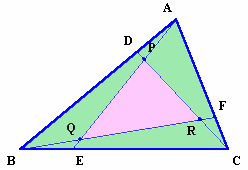２．解答例1

まず、各線分の長さの比を求めます。

求める方法としては、
　・三角形の面積比で考える
　・メネラウスの定理を用いる
　・ベクトルを用いる
などが考えられますが、ここではメネラウスの定理を用いることにしましょう。

図１
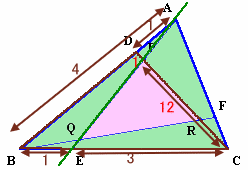
参考図1
△ＤＢＣと直線ＡＥについて、
メネラウスの定理より、
（ＤＡ／ＡＢ）・（ＢＥ／ＥＣ）・（ＣＰ／ＰＤ）＝１
（１／４）・（１／３）・（ＣＰ／ＰＤ）＝１
よって、ＣＰ：ＰＤ＝１２：１。　・・・　（１）
図２
参考図2
△ＡＤＣと直線ＢＦについて、メネラウスの定理より、
（ＡＢ／ＢＤ）・（ＤＲ／ＲＣ）・（ＣＦ／ＦＡ）＝１
（４／３）・（ＤＲ／ＲＣ）・（１／３）＝１
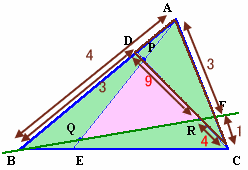
よって、ＤＲ：ＲＣ＝９：４。　・・・　（２）

（１）、（２）より、ＣＲ：ＲＰ：ＰＤ＝４：８：１。
同様にして、ＡＰ：ＰＱ：ＱＥ＝４：８：１、ＢＱ：ＱＲ：ＲＦ＝４：８：１。

図３
参考図3

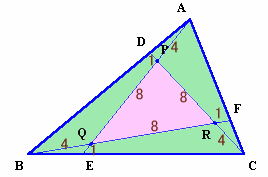
Ｓ＝△ＡＢＣとします。

△ＤＢＣ＝Ｓ×ＤＢ／ＡＢ＝Ｓ×３／４。
△ＤＢＲ＝△ＤＢＣ×９／１３＝Ｓ×（３／４）×（９／１３）。
△ＰＱＲ＝△ＤＢＲ×（ＰＲ／ＤＲ）×（ＱＲ／ＢＲ）
　　　　＝Ｓ×（３／４）×（９／１３）×（８／９）×（８／１２）
　　　　＝Ｓ×４／１３。

よって、△ＰＱＲ：△ＡＢＣ＝４：１３。

答：４：１３

以上　　

３．解答例２（Hamayanさん、他）

各線分の比を求めるところまでは、解答例１と同じ。

△ＰＱＲの各辺ＰＱ、ＱＲ、ＲＰの中点を結び△ＰＱＲを４等分します。
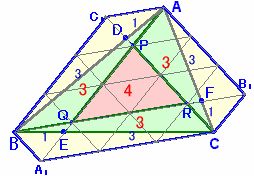
ｓ＝△ＰＱＲ／４とします。

図４
参考図4

解答例１図３のように各線分の比が求まっていますから、
Ａ、Ｐ、ＰＱの中点、Ｂ、Ｃを通り辺ＱＲに平行な直線、
Ｂ、Ｑ、ＱＲの中点、Ｃ、Ａを通り辺ＲＰに平行な直線、
Ｃ、Ｒ、ＲＰの中点、Ａ、Ｂを通り辺ＰＱに平行な直線を引くと
図４のようになります。

△ＡＢＱ＝平行四辺形ＡＣ1ＢＱ／２＝３ｓ、
△ＢＣＲ＝平行四辺形ＢＡ1ＣＲ／２＝３ｓ、
△ＣＡＲ＝平行四辺形ＣＢ1ＡＰ／２＝３ｓ。

よって、
△ＡＢＣ＝△ＰＱＲ＋△ＡＢＱ＋△ＢＣＲ＋△ＣＡＲ
　　　　＝４ｓ＋３ｓ＋３ｓ＋３ｓ＝１３ｓ。

従って、△ＰＱＲ：△ＡＢＣ＝４ｓ：１３ｓ＝４：１３。