第２１４問の解答

１．問題　［空間図形］

問題図
　左の図１は、部品Ａと部品Ｂでできたある立体の展開図です。

　図２のように、部品Ａを４つ使って正方形を作ると、その面積は４.５cm2となるそうです。
また、図１にもある通り、部品Ａを６つ用いて作った正六角形と、部品Ｂを６つ用いて作った正六角形を比較すると、面積比が３：１となっています。

　では、図１の展開図を組み立てて出来る立体の体積は何cm3でしょうか。

　

２．解答例１（まろやさん、うっしーさん、ταροさん、ありっちさん、ふきゅさん、長野美光さん、noetherさん、糸瀬善人さん、萬田銀次郎さん、M.Hossieさん、dragon-kさん、kazuyoさん、大沢幸一さん、mhayashiさん、他多数）

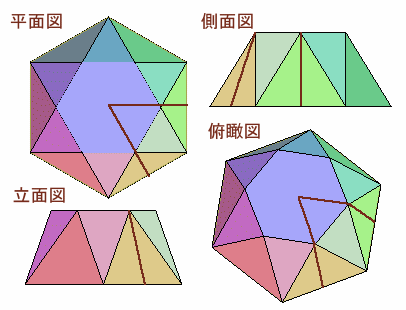
まず、求める立体の図を考えてみます。

参考図1

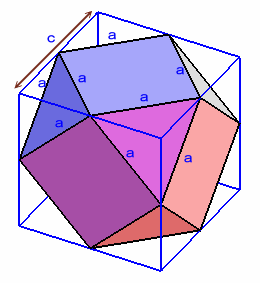
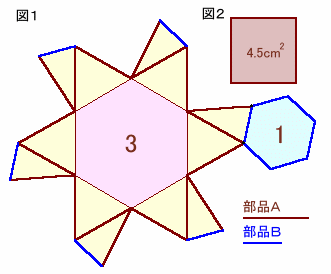
部品Ａの長さをａ、部品Ｂの長さをｂとすると、上図のように、
　底面：１辺の長さがａの正六角形
　頂面：１辺の長さがｂの正六角形
　側面：１辺の長さがａの正三角形、辺の長さがａ、ａ、ｂの二等辺三角形
から成り立ちます。
ただし、ｂ＝ａ／√3、ａ＝√（９/２）＝３/√2。

これをケーキのように６分の１をスライスします。
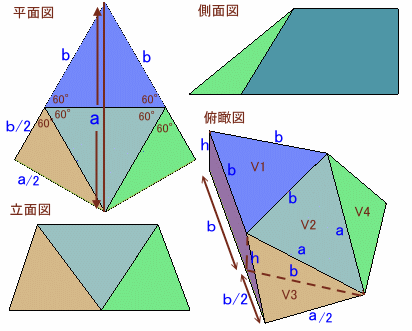
立体の高さをｈとすると、ｈは斜辺ａ、底辺ｂの直角三角形の１辺となるので、
　ｈ2＝ａ2−ｂ2、ｂ＝ａ／√3、よりｈ＝ａ×√6/3となります。

参考図2 参考図3

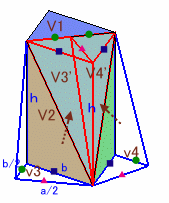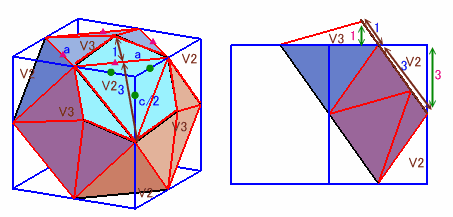
さらに、これを
　 V1：底面が１辺ｂの正三角形からなる三角柱
 　V2：底面が１辺ｂの正三角形からなる三角柱を切断したもの
 　V3、V4：底面がｂ、ｂ/2、ａ/2の直角三角形からなる三角錐
に分割する。

そして、V3、V4を移動して、V2の上に載せたものをV3'、V4'とすると、V2、V3'、V4'を合わせた立体はちょうどV1と同じ大きさの三角柱となります。

従って、求める立体の体積Ｖは、V1の体積の１２倍になります。
　V＝（1/2×ｂ×√3/2×ｂ）×ｈ×12
　　＝√3/4×ｂ2×ａ×√6/3×12
　　＝3√2×ａ3/3
　　＝√2×（3/√2）3
　　＝27/2ｃｍ3　となります。

答 27/2ｃｍ3

　以上

３．解答例２（ταροさん、沢井ねむ・るさん他）

第１３１回問題、第１５６回問題が参考になります。
対角線の長さが２ａとなる正方形の長さをｃとし、１辺の長さがｃの正六面体の各中点を結んで下図のような立体を考えます。
この立体の体積をＶ１とします。
　ｃ2＝２ａ２＝９より、ｃ＝３ｃｍ。

参考図4

この立体は、ほとんど求める立体に近く、下図のような四角錐３個を加えると、求める立体になります。

（参考：動く立体図）
参考図5

V1は、立方体の半分からV2を４個除いたもので、求める立体はV1にV3を３個加えたものになります。

V2は、底面が１辺c/2の二等辺三角形で、高さc/2の三角錐。
よって、
　V2＝1/2×(c/2)2×(c/2)×1/3
　　　＝c3×1/48。

V3は、底辺が１辺aの正方形で、高さはV2の高さの1/3。
よって、
　V3＝a2×(c/2)×1/3×1/3
　　　＝c2×1/2×(c/2)×1/3×1/3
　　　＝c3×1/36。

従って、V3＝V2×4/3。

求める立体の体積
　　　＝c3/2-V2×４＋V3×３
　　　＝c3/2
　　　＝27/2cm3　となります。　

４．解答例３（イデムリンさん、ヒデー王子さん、トトロ＠Ｎさん、祝いビルさん、他）

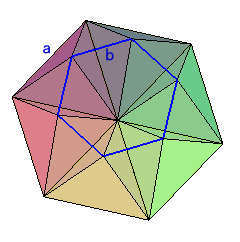
１辺がａの正四面体を６つならべ、各頂点を結ぶと求める立体になります

参考図6

解答例１と同様にして、求める立体の体積は、１辺がｂの六角柱の２倍、すなわち１辺がａの六角柱の２／３倍になります。

d=c/2とすると、正四面体の体積は、１辺ｄの立方体の体積の1/3＝d3/3。
　（d3-d3/6×４＝d3/3）

参考図１

正四面体と底面を共通にする三角柱の体積は、その３倍＝d3。

よって、求める立体の体積
　　＝d3×6×2/3
　　＝（3/2）3×4
　　＝27/2cm3。