第２９２問の解答

問題　［ 空間図形］

問題図

左図のような、体積が３２０cm3の正四面体ＡＢＣＤがあります。

いま、点Ｐを辺ＡＢ上に、点Ｑを辺ＢＣ上に、点Ｒを辺ＣＤ上に、点Ｓを辺ＤＡ上に、ＡＰ：ＰＢ＝ＢＱ：ＱＣ＝ＣＲ：ＲＤ＝ＤＳ：ＳＡ＝１：３となるようにとります。

このとき、四面体ＰＱＲＳの体積は何cm3でしょうか。

　

解答例１（トトロ＠Ｎさん、ミミズクはくず耳さん、CRYING DOLPHINさん、小西孝一さん、 他 多数）

参考図１

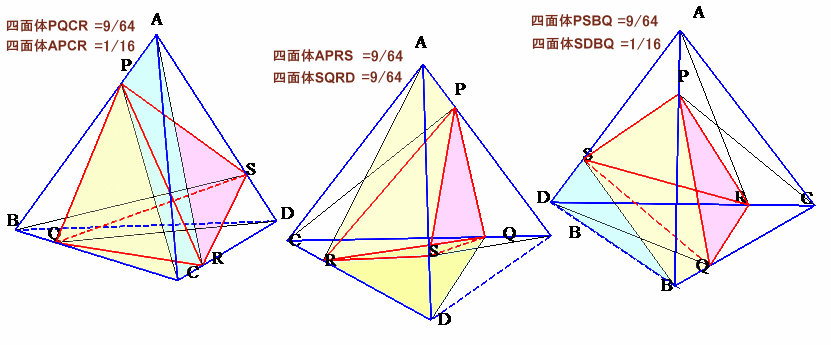
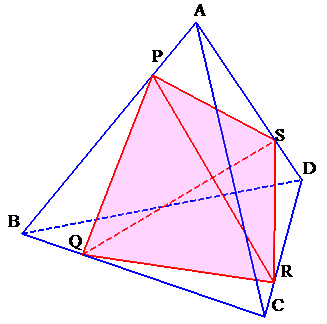
正四面体ＡＢＣＤから６つの四面体を切り取ると四面体ＰＱＲＳが残ります。

その６つの四面体の体積は、正四面体ＡＢＣＤの体積を１とすると、
　・四面体PQCR＝9/64、・四面体APCR＝1/16
　・四面体APRS＝9/64、・四面体SQRD＝9/64
　・四面体PSBQ＝9/64、・四面体SDBQ＝１/16
となります。

例えば、四面体PQCRは、
　底面の面積△PQC
＝△ABC−△PBC−△APC
＝△ABC×（１−1/4×3/4−1/4）
＝△ABC×9/16
　高さの比＝CR：CD＝１：４
より、正四面体ＡＢＣＤの9/16×1/4＝9/64。

また、四面体APCRは、
　底面の面積△APC＝△ABC×1/4
　高さの比＝CR：CD＝１：４
より、正四面体ＡＢＣＤの1/4×1/4＝1/16。

他の四面体も同様。

したがって、
　四面体ＰＱＲＳ
＝正四面体ＡＢＣＤ×（１−9/64×４−1/16×２）
＝正四面体ＡＢＣＤ×５/１６
＝３２０×５/１６
＝１００cm3
　となります。

答：１００cm3

以上

解答例２（まるケンさん、角田(＾＾)v鉄也さん、あんみつさん、 他）

正四面体ＡＢＣＤがすっぽり入る立方体をBB'AA'-C'CD'D、四面体ＰＱＲＳがすっぽり入る直方体をQQ'PP'-R'RS'Sとします。

参考図２D

よく知られたように（第１３１回問題、第１５６回問題）、
　正四面体ＡＢＣＤの体積＝立方体BB'AA'-C'CD'Dの体積×1/3　・・・　（１）
ですが、同様に
　四面体ＰＱＲＳの体積＝直方体QQ'PP'-R'RS'Sの体積×1/3　・・・（２）
も成り立ちます。

よって、（１）、（２）より、
　正四面体ＡＢＣＤ：四面体ＰＱＲＳ
＝立方体BB'AA'-C'CD'D：直方体QQ'PP'-R'RS'S　・・・　（３）
となります。

さて、直方体の底面Q'RS'Pは正方形で、正方形B'CD'Aより面積が1/4×3/4×1/2=3/32の三角形４個を除いたものになるので、
　Q'RS'P＝B'CD'A×（１−3/32×４）＝B'CD'A×５/８　
　高さPP'＝AA'×１/２　
より、
　直方体QQ'PP'-R'RS'S＝立方体BB'AA'-C'CD'D×５/１６。

よって、（３）より、
　四面体ＰＱＲＳ
＝正四面体ＡＢＣＤ×５/１６
＝３２０cm3×５/１６
＝１００cm3
となります。

（参考）動く３D図

（その他の解法）

・適当に補助線引いて切断　・・・ねこやんさん
　元の三角錐の２２／６４の図形が２つできるので（１−４４／６４）×３２０＝１００

・三角比、ベクトル、座標等で計算　・・・
　QPerさん、sodoさん、Mikiさん、Taroさん、takuさん、sugitakukunさん、海栗さん、長野美光さん、有無相生さん、M.Hossieさん、モルモット大臣さん、ふじさきたつみさん、他