第３１５問の解答

---

問題　［空間図形］

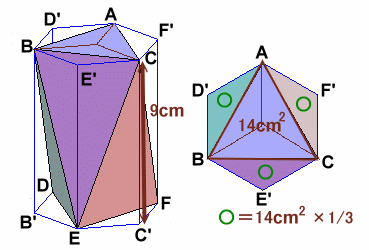
		左図のような、高さ９cmの円柱があります。 いま、円柱の上面に正三角形ＡＢＣを、下面に正三角形ＤＥＦを、上から見たところが右の図のようになるようにとりました。（点Ｄ、Ｅ、Ｆはそれぞれ弧ＡＢ、弧ＢＣ、弧ＣＡの中点です。） また、正三角形ＡＢＣの面積は１４cm2となっています。 このとき、図の立体（面が全て三角形の８面体）の体積を求めて下さい。

---

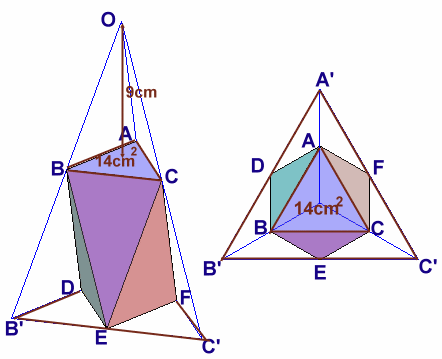
解答例１

暇な人間さん、Banyanyanさん、トトロ＠Ｎさん、ねこやんさん、Taroさん、ふじさきたつみさん、M.Hossieさん、kokoさん 、あんみつさん、小西孝一さん、ωさん、あやのりんさん、大岡　敏幸さん、 他 多数

	下図のように、問題の立体は正六角柱にすっぽり入ります。（参考：２１４回問題） 正六角柱の上面・下面である正六角形の面積は、正三角形ABCの２倍＝２８cm3。 問題の立体は、この正六角柱から全て同じ大きさの三角錐六個を除いたものになっています。 また、この三角錐の底面は、正三角形の1/3で、高さは正六角柱と同じ９cm。 従って、求める立体の体積は、 　２８×９−1/3×（1/3×１４）×９×６ ＝２８×９×2/3 ＝１６８cm3。 答：　１６８cm3 以上

---

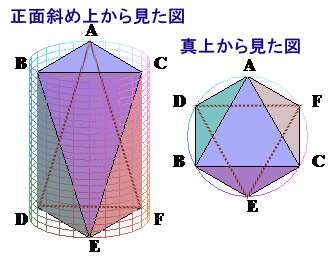
解答例２

CRYING DOLPHINさん、mhayashiさん、ミミズクはくず耳さん、高橋　道広さん、長野美光さん、 他

	下図のように底面がDEFの縦横２倍となる正三角形で、高さが求める立体の倍となる正三角錐を考えます。 求める立体は、この正三角錐から、底面がDEFと同じ正三角形で、高さが求める立体と同じ正三角錐を４個取り除いたものとなっています。 従って、体積＝1/3×（１４×４）×（９×２）−（1/3×１４×９）×４＝３３６−１６８＝１６８cm3。 （参考）「正四面体の４隅（４つの頂点）から、半分の大きさ（体積1/8）の正四面体４つを 切り落とすと正８面体ができる。（第１３１問・解答例２）」

---

（その他の解法）

• ACDEで二つに分けて求める　・・・　永井暁さん、 他
• 積分、シンプソンの法則で計算する　・・・　小杉原 啓さん、有無相生さん、中村明海さん、他
• 三角形の重なりでできる六角形を底辺とする六角柱と２種類の四角錐３個ずつ二分けて計算する　・・・　うのたかはるさん、あさみかずみさん、他
• ２つの三角錐と２つに四面体に分けて計算する　・・・　フランク長いさん、他