第３８７問の解答

問題［場合の数］

問題図

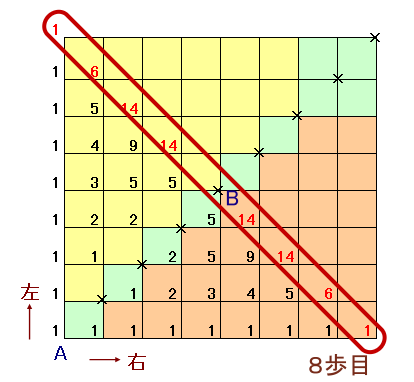
左図のような一本道のＡ地点にマサルさんがいます。定例呑み会後で酔っ払っているマサルさんは、１秒ごとに右か左のどちらかに一歩進みます。

では、マサルさんがＡ地点を出発点にして８秒間歩くとき、その途中で１度以上Ａ地点に戻っているような歩き方は何通りあるでしょうか。ただし、マサルさんの「一歩」は常に一定の長さであるものとします。

解答例１

ほげさん、UnderBirdさん、M.Hossieさん、寝不足文君さん、遠い山のぽきょぽんさん、linearsupertrainさん、
 小学名探偵さん、takaisaさん、あ〜く＠旧Ｎさん、なかさん、他他

A地点へ一度も戻らない場合の数を求めます。

参考図１

上図のような格子状の経路図で

  • マサルさんがAから右へ歩く←→経路図で右へ進む

  • マサルさんがAから左へ歩く←→経路図で上へ進む

と対応させると、A地点に戻ることは、経路図では対角線AB上の格子点を通ることになります。

従って、これらの格子点を通らない場合を経路図で順に数え上げていくと、
　８歩目＝１＋６＋１４＋１４＋１４＋１４＋６＋１＝７０通り
となります。

１歩毎にマサルさんは、右左２通りの歩き方があるので、
　８歩目合計＝２8＝２５６通り
になります。

よって、
　A地点に１度以上戻る歩き方＝２５６−７０＝１８６通り
と求まります。

答：　１８６通り

以上

解答例２

ほげさん、トトロ＠Ｎさん、小西孝一さん、ミミズクはくず耳さん、とまぴょんさん、他多数

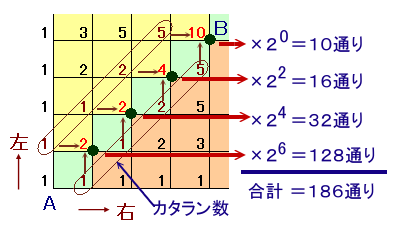
初めてA地点に戻るまでの歩数で場合分けします。

参考図２

  • ２歩でもどるとき　・・・　１×２×２6＝１２８通り

  • ４歩でもどるとき　・・・　１×２×２4＝　３２通り

  • ６歩でもどるとき　・・・　２×２×２2＝　１６通り

  • ８歩でもどるとき　・・・　５×２×２0＝　１０通り

従って、
　合計＝１２８＋３２＋１６＋１０＝１８６通り
と求まります。

（参考）一般式　・・・　小学名探偵さん、他

本問を２n歩のときに拡張したときの場合をSnとすると、
　Sn＝２2n−2nCn ・・・　（１）
と表すことができます。
これを数学的帰納法で示します。　

上記より、
　Sn＝Σ(k＝0..n-1){2kCk/(k+1)×２2(n-k)-1}
となります。

まず、S1＝２、および２2−2C1 ＝２より、（１）式は成り立ちます。

（１）式がSnまで成り立つとしたとき、
　Sn+1＝Σ(k＝0..n){2kCk/(k+1)×２2(n+1-k)-1}
　　　＝Σ(k＝0..n-1){2kCk/(k+1)×２2(n-k)-1}×４＋2nCn/(n+1)×２
　　　＝Sn×４＋2nCn/(n+1)×２
　　　＝（２2n−2nCn）×４ ＋2nCn/(n＋1)×２
　　　＝２2n+2−｛2nCn×４（n＋1)-２｝/(n＋1)
　　　＝２2n+2−｛2nCn×（２n＋２）（２n＋1)｝/｛(n＋1)(n＋1)｝
　　　＝２2n+2−2n+2Cn+1
となり、Sn+1についても（１）式が成り立つことになります。

以上により、帰納法にて（１）式が成り立つことが示されました。

（別解）

（１）式から、解答例１で求めたA地点へ一度も戻らない場合の数と、
ちょうど２n歩でA地点に戻る場合の数2nCn が等しいことが分かります。

このことについても小学名探偵さんは経路図の乗り換え法（参考：第３３０問）を応用して示されました 。当初、当方の理解不足で掲載することを断念しましたが、ようやく理解できましたので、こちらに掲載いたしました。

よろしくお願いいたします。

（その他の解法）