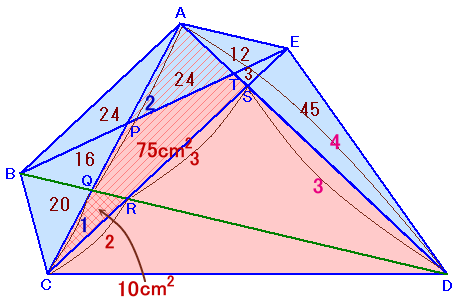
第４１９問の解答

問題［平面図形］

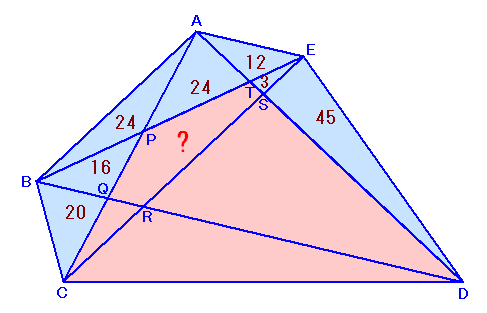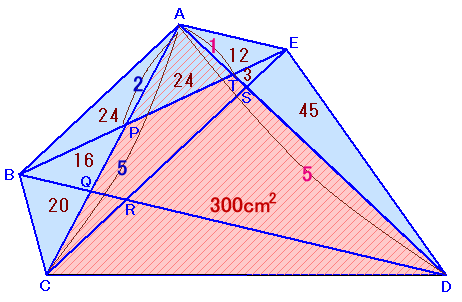
左図のような五角形ＡＢＣＤＥがあります。図中の数字は、対角線によって五角形が分割されてできた各三角形の面積
を表しています。

このとき、
　（１）　四角形ＰＣＤＴの面積（ピンク色の部分）
　（２）　五角形ＰＱＲＳＴの面積（？の部分）
を求めてください。

解答例１

Gouさん、あ～く＠ぴかぴかの（略さん、姉小路さん、トトロ＠Ｎさん、CRYING DOLPHINさん、ゴンともさん、ミミズクはくず耳さん、M.Hossieさん、みかんさん、カゲコさん、あさみかずみさん、他多数

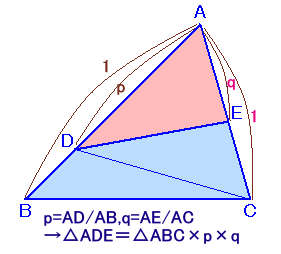
（補題）△ABCの辺AB上の点D、AC上の点Eに関して、
△ADE＝△ABC×AD/AB×AE/AC（証明はこちら）

　

補題を用いて、△ACDの面積を求めてみましょう。

△BAP、△BPQ、△BQCは、高さが共通なので面積は底辺の長さの比に等しい。
よって、
　AP：PQ：QC＝２４：１６：２０＝６：４：５ 　・・・　（１）

同様に、
　　AT：TS：SD＝１２：３：４５＝４：１：１５ 　・・・　（２）

補題より、
　△APT＝△ACD×AP/AC×AT/AD
　　２４＝△ACD×６/１５×４/２０
　　　　＝△ACD×２/２５

よって、
　△ACD＝２４×２５/２＝３００cm²　

従って、
　四角形PCDT＝△ACD－△APT＝３００－２４＝２７６cm²
と求まります。
　

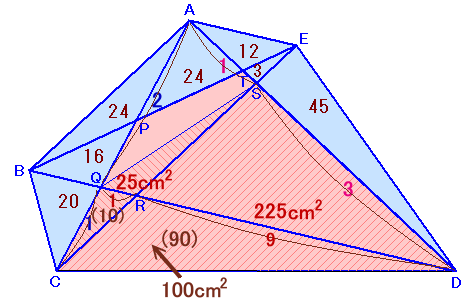
面積比を用いて、△QCRの面積を求めてみましょう。

QとSを結び、三角形を分割して考えます。

まず、　△ACS：△SCD＝AS：SD＝５：１５＝１：３、
よって、
　△ACS＝△ACD×1/4＝３００×1/4＝７５cm²　
　△SCD＝△ACD×３/4＝３００×1/4＝２２５cm²　・・・　（３）

次に、
　△SAQ：△SQC＝AQ:QC＝１０：５＝２：１
よって、
　△AQS＝△ACS×1/３＝７５×２/３＝５０cm²　
　△QCE＝△ACS×３/4＝７５×1/３＝２５cm²　・・・　（４）

（３）、（４）より、　
　QR：RD＝△SQR：△SCD＝２５：２２５＝１：９　・・・　（５）

さて、　△AQD：△QCD＝AQ：QC＝２：１、
よって、
　△AQD＝△ACD×２/３＝３００×２/３＝２００cm²　
　△QCD＝△ACD×１/３＝３００×1/３＝１００cm²　・・・　（６）　

（５）、（６）より、
　△QCR：△RCD＝QR：RD＝１：９、
よって、
　△QCR＝△QCD×１/１０＝１００×１/１０＝１０cm²　・・・　（７）　
　△RCD＝△QCD×９/１０＝１００×９/１０＝９０cm²　　

以上より、
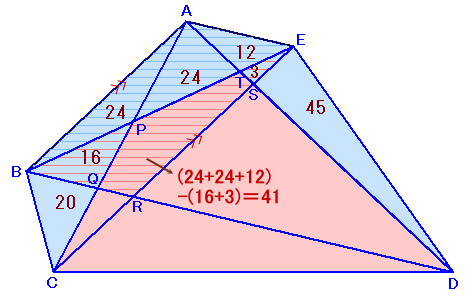
　五角形ＰＱＲＳＴ
＝△ACS－△APT－△QCR
＝７５－２４－１０
＝４１cm²
と求まります。

答：　（１）２７６cm²（２）４１cm²

以上

解答例２

きょろ文さん、他

（１）は、解答例１と皆さんほぼ同じなので、以下では、（２）について解答例を紹介いたします。

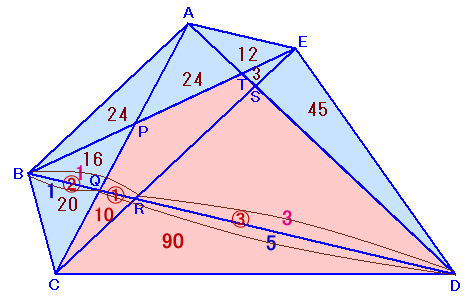
BR：QR：RDを求めてみましょう。

まず、
　BQ：QD＝△ABC：△ACD＝６０：３００＝１：５　・・・　（１）

次に、
　△EBC＝△ACD－△APT＋△ETS＋△PBC＝７５－２４＋３＋３６＝９０cm²
　△ECD＝△SCD＋△ESD＝２２５＋４５＝２７０cm²よって、
　BR：RD＝△EBC：△ECD＝９０：２７０＝１：３　・・・　（２）

（１）より、BQ：QD＝２：１０
（２）より、BR：RD＝３：９
よって、BR：QR：RD＝２：１：９　・・・　（３）

（３）より、
　△BCQ：△QCR：△RCD＝BR：QR：RD
よって、
　△QCR＝△BCQ×１/２＝２０×１/２＝１０cm²
　
従って、
　五角形ＰＱＲＳＴ
＝△ACS－△APT－△QCR
＝７５－２４－１０
＝４１cm²
と求まります。

解答例３

uchinyanさん、他

△ACSと直線BDに関してメネラウスの定理より、
　AQ/QC×CR/RS×SD/DA＝１

　（２４＋１６）/２０×CR/RS×４５/（４５＋３＋１２）＝１
よって、
　CR/RS＝１/２×４/３＝２/３

従って補題より、
　△QCR＝△ACS×CQ/CA×CR/CE＝７５×１/３×２/５＝１０cm²

従って、
　五角形ＰＱＲＳＴ
＝△ACS－△APT－△QCR
＝７５－２４－１０
＝４１cm²
と求まります。

解答例４

おかひで博士さん、鉄腕アトムでーすさん、スモークマンさん、cresta97gx100さん、りえパパさん、他

四角形ABREが平行四辺形であることを利用します。

△EAB＝１２＋２４＋２４＝６０cm²、
△CAB＝２４＋１６＋２０＝６０cm²、
よって、△EAB＝△CAB。

△EABと△CABは、底辺が共通だから高さが等しいことが分かります。
従って、ABとECは平行となります。

次に、
△BAE＝１２＋２４＋２４＝６０cm²、
△DAE＝１２＋３＋４５＝６０cm²、
よって、△BAE＝△DAE。

従って、同様にしてAEとBDが平行となります。

よって、四角形ABREは平行四辺形となります。

すると、
　△EBR＝△BAE＝６０cm²、
よって、
　五角形ＰＱＲＳＴ
＝６０－１６－３
＝４１cm²
と求まります。


	（１）は、解答例１と皆さんほぼ同じなので、以下では、（２）について解答例を紹介いたします。 BR：QR：RDを求めてみましょう。まず、　BQ：QD＝△ABC：△ACD＝６０：３００＝１：５　・・・　（１）次に、　△EBC＝△ACD－△APT＋△ETS＋△PBC＝７５－２４＋３＋３６＝９０cm² 　△ECD＝△SCD＋△ESD＝２２５＋４５＝２７０cm²よって、　BR：RD＝△EBC：△ECD＝９０：２７０＝１：３　・・・　（２）（１）より、BQ：QD＝２：１０（２）より、BR：RD＝３：９よって、BR：QR：RD＝２：１：９　・・・　（３）（３）より、　△BCQ：△QCR：△RCD＝BR：QR：RD よって、　△QCR＝△BCQ×１/２＝２０×１/２＝１０cm² 　従って、　五角形ＰＱＲＳＴ＝△ACS－△APT－△QCR ＝７５－２４－１０＝４１cm² と求まります。


	△ACSと直線BDに関してメネラウスの定理より、　AQ/QC×CR/RS×SD/DA＝１　（２４＋１６）/２０×CR/RS×４５/（４５＋３＋１２）＝１よって、　CR/RS＝１/２×４/３＝２/３従って補題より、　△QCR＝△ACS×CQ/CA×CR/CE＝７５×１/３×２/５＝１０cm² 従って、　五角形ＰＱＲＳＴ＝△ACS－△APT－△QCR ＝７５－２４－１０＝４１cm² と求まります。


	四角形ABREが平行四辺形であることを利用します。 △EAB＝１２＋２４＋２４＝６０cm²、 △CAB＝２４＋１６＋２０＝６０cm²、よって、△EAB＝△CAB。 △EABと△CABは、底辺が共通だから高さが等しいことが分かります。従って、ABとECは平行となります。次に、 △BAE＝１２＋２４＋２４＝６０cm²、 △DAE＝１２＋３＋４５＝６０cm²、よって、△BAE＝△DAE。従って、同様にしてAEとBDが平行となります。よって、四角形ABREは平行四辺形となります。すると、　△EBR＝△BAE＝６０cm²、よって、　五角形ＰＱＲＳＴ＝６０－１６－３＝４１cm² と求まります。