第434問の解答
問題[平面図形]
|
|
|
|
|
|
|
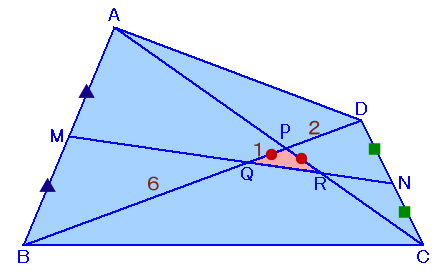 |
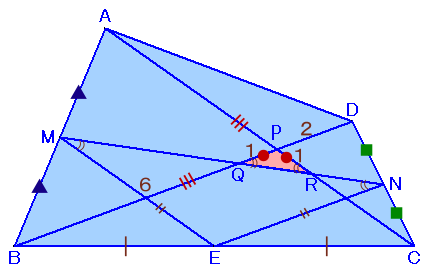
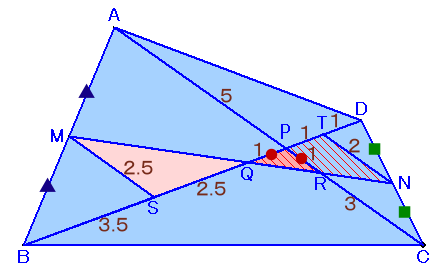
左図のような四角形ABCDがあり、ABの中点をM、CDの中点をNとします。 いま、MNと対角線AC、BDの交点をそれぞれR、Q、ACとBDの交点をPとします。すると、PQ=PR、BQ:QP:PD=6:1:2となりました。 このとき、四角形ABCDの面積は、△PQRの面積の何倍か求めてください。 |
|
|
|
|
|
|
解答例1
マサルさん、uchinyanさん、他
辺BCの中点をEとします。
△BEMと△BCAについて中点連結定理より、
EMとCAは平行、EM=CA×1/2 ・・・ (1)
△CNEと△CDBについて中点連結定理より、
NEとDBは平行、NE=DB×1/2 ・・・ (2)
となります。(1)より、EMとCAが平行だから、∠EMN=∠PRQ(錯角)
(2)より、NEとDBが平行だから、∠ENM=∠PQR(錯角)
ところが、△PQRはPQ=PRの二等辺三角形なので、∠PRQ=∠PQR、
よって、∠EMN=∠ENMとなるので、
△ENMも△PQRと相似でEM=ENの二等辺三角形と分かります。従って、(1)、(2)より、CA=BDとなります。
高さが同じ三角形の面積比=底辺の長さの比より、△PQRの面積を1とすると、
△RPB=△PQR×PB/PQ=7
△CBA=△RPB×CA/PR=7×9=63 ・・・ (3)
また、
△RDP=△PQR×DP/PQ=2
△CAC=△RDP×CA/PR=2×9=18 ・・・ (4)よって、(3)、(4)より、
四角形ABCD=△CBA+△CAC=63+18=81
と求まります。答: 81倍
以上
解答例2
姉小路さん、あーく@19さん、他
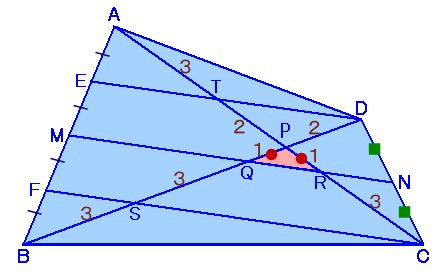
Dを通りNMと平行に引いた直線とABの交点をE、ACとの交点をTとし、
Cを通りNMと平行に引いた直線とABの交点をF、ACとの交点をSとします。
△DQNと△DSCについて中点連結定理より、DQ=QS、
よって、PQの長さを1とすると、
QS=DQ=PQ+DP=1+2=3
従って、
SB=BQ−QS=6−3=3QRとSCが平行より、△PQRと△PSCは相似、
従って、PR:RC=PQ:QS=1:3、よって、RC=3。また、QRとTDが平行より、△PQRと△PDTは相似、
従って、PR:PT=PQ:PD=1:2、よって、PT=2。さらに、SFとQM、DEが平行より、△BSF△BQMおよび△BDEは相似、
従って、BF:FM:ME=BS:SQ:QD=3:3:3=1:1:1、
ところがMA=BMだから、ME=MA×1/2=EAとなります。最後に、△AETと△ANRについて中点連結定理より、
AT=TR=PT+PR=2+1=3以上から、AC=AT+TP+PR+RC=3+2+1+3=9
となります。以下、解答例1と同様。
解答例3
トロ@Nさん、みかんさん、 他
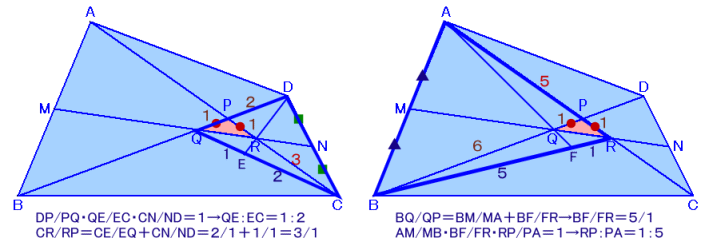
△DQCに関してチェバの定理より、
DP/PQ・QE/EC・CN/ND=1、
2/1・QE/EC・1/1=1、
よって、QE:EC=1:2。すると、チェバの定理の補題より、
CR/RP=CE/EQ+CN/DN=2/1+1/1=3
よって、PRの長さを1とすると、CR=3となります。また、△ABRに関してチェバの定理の補題より、
BQ/QP=BM/MA+BF/FR=1/1+BF/FR=6/1、
BF/FR=5、
よって、BF:FR=5:1。すると、チェバの定理より、
AM/MB・BF/FR・RP/PA=1、
1/1・5/1・RP/PA=1
RP/PA=5
よって、PA=5となります。以上から、AC=AT+TP+PR+RC=3+2+1+3=9
となり、以下同様。
解答例4
アヒーのおじさんさん、uchinyanさん、ヤッコチャさん、kaizer YSさん、N.Nishiさん、他
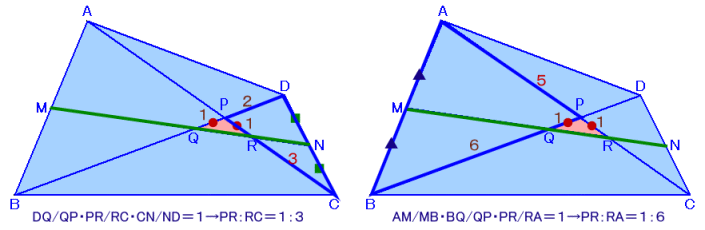
△DPCと直線MNに関してメネラウスの定理より、
DQ/QP・PR/RC・CN/ND=1、
3/1・PR/RC・1/1=1、
よって、PR/RC=1/3、RC=3となります。また、△ABPと直線MNに関してメネラウスの定理より、
AM/MB・BQ/QP・PR/RA=1、
1/1・6/1・PR/RA=1、
よって、PR/RA=1/6、RA=6、
従って、PA=RA−PR=5となります。以上から、AC=AT+TP+PR+RC=3+2+1+3=9
となり、以下同様。
解答例5
エルクさん、他
中点Nを通りACと平行に引いた直線とBDの交点をT、
中点Mを通りACと平行に引いた直線とBDの交点をSとします。
△BPAに関し中点連結定理より、BS=SP、
BS+SP=BQ+QP=6+1=7だから、
BS=SP=3.5、SQ=BQ−BS=6−3.5=2.5
となります。次に、PRとMSが平行だから、△SQMと△PQRは相似、
よって、MS:PR=SQ:PQ=2.5:1、MS=2.5。さきほどの△BPAに関した中点連結定理より、
AP=MS×2=2.5×2=5。また、△DPCに関し中点連結定理より、DT=PT、
DT+PT=PD=2だから、
DT=PT=1
となります。すると、△QNTに関し中点連結定理より、
TN=PR×2=2。よって、△DPCに関し中点連結定理より、
PC=TN×2=4、RC=PC−PR=3。以下、同様。
解答例6
あさみかずみさん、他
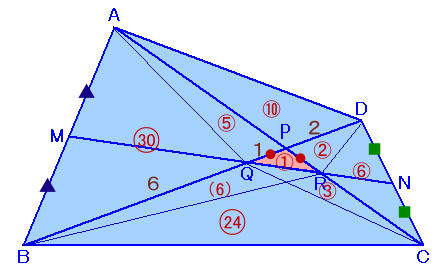
高さが同じ三角形の面積比=底辺の長さの比より、△PQRの面積を1とすると、
△RDP=△PQR×DP/PQ=1×2/1=2。また、
△CQR=△DQR×CN/DN=3×1/1=3、
△CDR=△CQR×DP/PQ=3×2/1=6、
△CQB=△CPQ×BQ/PQ=4×6/1=24。今度は、△RBQ=△PQR×BQ/PQ=1×6/1=6、
よって、△AQR=△BQR×BM/AM=6×1/1=6、
従って、△AQP=△AQRー△PQR=6−1=5。また、
△ABQ=△AQP×BQ/PQ=5×6/1=30、
△APD=△AQP×PD/PQ=5×2/1=10。以上から、
四角形ABCD
=△ABQ+△AQP+△APD+△CBQ+△CQR+△PQR+△CRD+△RPD
=30+5+10+24+3+1+6+2=81
と求まります。
解答例7
小学名探偵さん、他
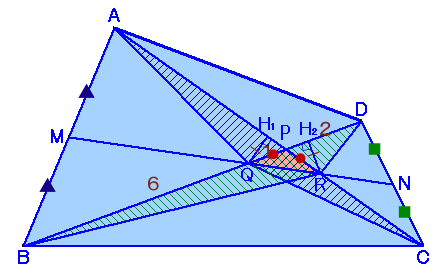
QからACに下ろした垂線の足をH1、RからBDに下ろした垂線の足をH2とします。
PQ=PR、∠QPH1=∠RPH2、∠QH1P=∠RH2P=90°より、
△QPH1と△RPH2は相似な直角三角形、
よって、QH1=RH2。従って、
△QCA:△RDB
=1/2×AC×QH1:1/2×BD×RH2
=AC:BD ・・・ (1)
となります。また、高さが同じ三角形の面積比=底辺の長さの比より、
△AQR:△BQR=AM:BM=1:1
よって、△AQR=△BQR。 ・・・ (2)同様に、△DQR=△CQR。 ・・・ (3)
よって、(2)、(3)より、
△QCA=△AQR+△CQR=△BQR+△DQR=△RDB ・・・ (4)従って、(1)、(4)より、AC=BDとなります。
以下、同様。
(その他の解法)
CADなどで作図して求める ・・・ kasamaさん、圭太さん、他
座標で表して方程式を解く ・・・ Toru Fukatsuさん、他