問題[平面図形]
|
|
|
|
|
|
|
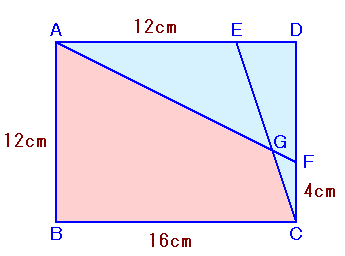 |
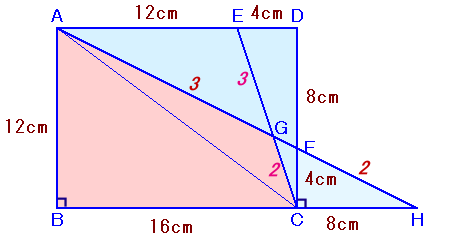
左図のABCDは長方形です。 四角形ABCG(斜線部分)の面積は何cm2になりますか? |
|
|
|
|
|
|
解答例1[AFを延長する、ビシュッと]
| あまれっとさん、Nなヒトさん、ziziさん、ヌオさん、浜直君さん、 elmotitiさん、サラのパパさん、 ライスさん、他 |
AFを延長してBCと交わった点をHとします。
ABとFCは平行だから、△ABHと△FCHは相似で、
相似比はFC:AB=4:12=1:3。
従って、HC:HB=1:3、HC:CB=1:2、
よって、HC=BC×1/2=16×1/2=8cm。次に、AEとHCは平行だから、△AEGと△HCGは相似で、
相似比はAE:HC=12:8=3:2、
よって、cm2。 となります。 ・・・ (1)△ACH=1/2×CH×CD=1/2×8×12=48cm2。
△ACHの底辺をAHと考えれば、
△CAG:△CGH=AG:GH=3:2。よって、△AGC=△ACH×3/5=48×0.6=28.8cm2。
また、△ABC=1/2×BC×AB=1/2×16×12=96cm2。
従って、四角形ABCG=△ABC+△AGC=96+28.8=124.8cm2
と求まります。答 124.8cm2
以上
(類解1)
同様に、EG:GC=3:2、
よって、
△GCF=△CED×2/5×4/12=24×2/15=3.2cm2。
また、台形ABCF=1/2×(12+4)×12=128cm2。
四角形ABCG=台形ABCF−△GCF=128−3.2=124.8cm2。
(類解2)
同様に、
△HGC=△HAB×2/5×8/24=144×2/15=19.2cm2。
四角形ABCG=△HAB−△HGC=144−19.2=124.8cm2。
解答例2[相似な図形:]
| ぺんこさん、Knightさん、大岡 敏幸さん、Yyukomamaさん、マナブさん、 Junkoさん、他 |
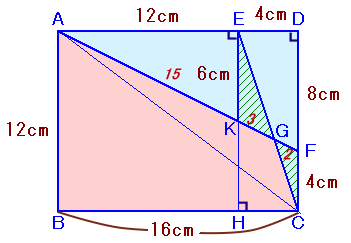
EからBCに下ろした垂線の足をHとし、EHとAFの交点をKとにします。
EKとDFは平行だから、△AEKと△ADFは相似で、
相似比=AE:AD=12:16=3:4。
よって、EK=DF×3/4=12×3/4=6cm。また、△GEKと△GCFも相似で、相似比=EK:CF=6:4=3:2 ・・・ (2)。
以下は、解答例1の各解法と同様にしても求められますが、ここでは次のようにしましょう。(2)より、KG:GF=3:2。
また、△AEKと△ADFの相似より、AK:KF=3:1、
従って、AK:KG:GF=15:3:2、
よって、AG:GF=18:2=9:1。△AGC=△AFC×9/10=32×0.9=28.8cm2。
従って、四角形ABCG=△ABC+△AGC=96+28.8=124.8cm2
と求まります。
解答例3[ベンツ切り]
| ティーハラさん、TORAさん、shuさん、他 |
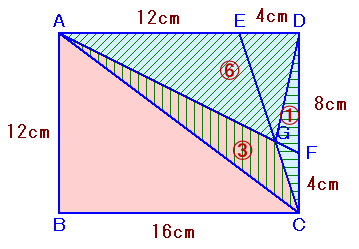
Gを中心にして△ACDを△ACG、△CDG、△DAGの3つに分割し、これらの面積比を求めます。
まず、△ACGと△CDGについて、
△ACE:△CDE=△GAE:△GDE=AE:DE=3:1。
よって、△ACG:△CDG=(△ACE−△GAE):(△CDE−△GDE)=3:1 ・・・ (1)同様に、△ACG:△DAG=(△ACF−△GCF):(△ADF−△GDF)=2:1 ・・・ (2)
よって、(1)、(2)より、
△ACG:△CDG:△DAG=3:1:6と求まります。従って、△ACG=△ACD×3/10=96×0.3=28.8cm2。
従って、四角形ABCG=△ABC+△ACG=96+28.8=124.8cm2
と求まります。(参考)
なお、(1)、(2)の求め方は、チェバの定理の証明で使用されており、
これらから、
AG:GF=△ACG+△DAG:△CDG=9:1
CG:GE=△ACG+△CDG:△DAG=2:3
が得られます。
解答例4[メネラウスの定理]
| ちずさん、長野 美光さん、N.Nishiさん、他 |
解答例3の参考の部分をメネラウスの定理を用いて求めます。
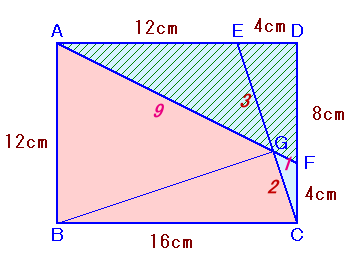
△AFDと直線FCに関してメネラウスの定理より、
AG/GF×FC/CD×DE/EA=1、
AG/GF×4/12×4/12=1、
よって、AG:GF=9:1。また、△CEDと直線FAに関してメネラウスの定理より、
EG/GC×CF/FD×DA/AE=1、
EG/GC×4/8×16/12=1、
よって、EG:GC=3:2。さて、
△GAB=△AFB×9/10=△ABC×9/10 ・・・ (1)
△GBC=△EBC×2/5=△ABC×2/5 ・・・ (2)(1)、(2)より、
四角形ABCG
=△GAB+△GBC
=△ABC×(0.9+0.4)
=96×1.3
=124.8cm2
と求まります。
(その他の解法)
- 座標をつかって点Gをもとめる ・・・ ショウさん、まるケンさん、MrYutaさん、午年のうりぼうさん、 辻さん、みかんさん、ちこりんさん、川村 高雅さん、tomhさん、 shiaroさん、kasamaさん、アラちゃんさん、 他
- 実際に作図した ・・・ 智乃介さん、沙月さん、 他