第３９７問の解答

問題［推理］

マサルさんは、１ｇ、４ｇ、アｇ、イｇの４種類の重りをそれぞれ１個ずつ持っています。（ただし、ア＜イとします）

これらの重りと天秤を使うと、ウｇまでの重さを１ｇ単位で全て量ることができるそうです。ただし、重りは天秤の両
側に載せることができます。

このとき、ウが最も大きくなるように、ア、イ、ウを求めて答えてください。

解答例１

まるケンさん、小学名探偵さん、はなうさん、圭太さん、CRYING DOLPHINさん、きょろ文さん、M.Hossieさん、 他

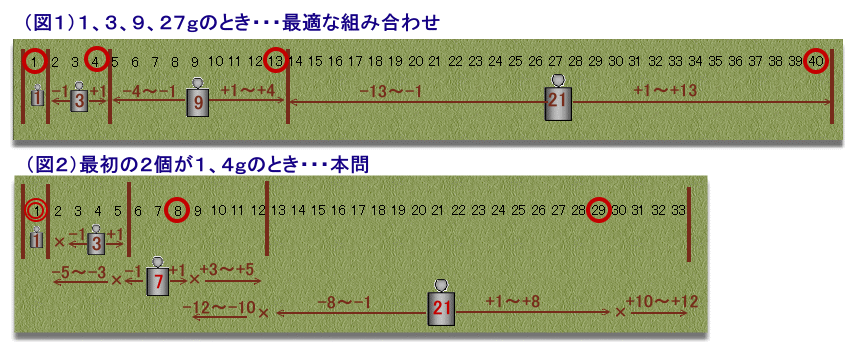
図１のように、１、３、９、２７ｇの４個の重りだと、１〜４０ｇの重さを１ｇ単位で全て量ることができます。
（算チャレ第７１問、算チャレVer.3第１０７問、数学の小部屋第２問）

参考図１

本問のように、最初の２個の重り（１ｇと３ｇ）では、１ｇ、３〜５ｇの４通りを量ることができます。

３番目の重り（アｇ）を加えると、さらにアｇおよびアｇ−（１ｇ、３〜５ｇ）、アｇ＋（１ｇ、３〜５ｇ）を量ることができます。
このとき、重り２個のときに抜けていた２ｇを量るとともに、１ｇ単位でできるだけ多くの重さを量ることを可能にするには、
（ア−５）ｇ＝２ｇ、すなわちア＝７とすれば良いことが分かります。

このとき、１ｇ、４ｇ、７ｇの３個で１ｇ〜８ｇ、および１０ｇ〜１２ｇを量ることが可能です。

同様に、４番目の重り（イｇ）を加えると、さらにイｇおよびイｇ−（１〜８ｇ、１０〜１２ｇ）、イｇ＋（１〜８ｇ、１０〜１２ｇ）を量ることができます。
このとき、重り３個のときに抜けていた９ｇを量るとともに、１ｇ単位でできるだけ多くの重さを量ることを可能にするには、
（イ−１２）ｇ＝９ｇ、すなわちイ＝２１とすれば良いことが分かります。

このとき、１ｇ、４ｇ、７ｇ、および２１ｇの４個で１ｇ〜２９ｇ、および３０ｇ〜３３ｇを量ることが可能です。
従って、ウ＝２９と分かります。

答：　ア＝７、イ＝２１、ウ＝２９

以上

（その他の解法）